题目内容
6．若点（a，b）在曲线$\frac{{x}^{2}}{b}$+$\frac{{y}^{2}}{a}$=0上，则a，b满足的条件是a+b=0．分析 把点（a，b）代入曲线$\frac{{x}^{2}}{b}$+$\frac{{y}^{2}}{a}$=0，可得$\frac{{a}^{2}}{b}+\frac{{b}^{2}}{a}$=0，化简整理即可得出．
解答 解：把点（a，b）代入曲线$\frac{{x}^{2}}{b}$+$\frac{{y}^{2}}{a}$=0，可得$\frac{{a}^{2}}{b}+\frac{{b}^{2}}{a}$=0，
化为a3+b3=0，
∴（a+b）（a2-ab+b2）=0，
∵a2-ab+b2=$（a-\frac{1}{2}b）^{2}$+$\frac{3{b}^{2}}{4}$≥0，
∴a+b=0．
∴a，b满足的条件是a+b=0．
故答案为：a+b=0．
点评 本题考查了点与曲线的关系、代数式的化简整理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
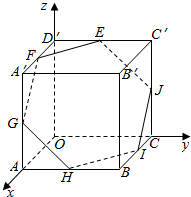正方体OABC-D′A′B′C′的棱长为a，E，F，G，H，I，J分别是棱C′D′，D′A′，A′A，AB，BC，CC′的中点，写出正六边形EFGHIJ各顶点的坐际．
金红石（TiO2）的晶胞如图所示，图中色点代表钛原子，黑点代表氧原子．长方体的8个顶点和中心是钛原子，4个氧原子的位置是A（0.31a，0.31b，0），B（0.69a，0.69b，0），C（0.81a，0，0.5c）和D（0.19a，0.81b，0.5c）．中心处钛原子与A处氧原子间的距离叫做键长．当a=b时，试求键长．