题目内容
18. 金红石(TiO2)的晶胞如图所示,图中色点代表钛原子,黑点代表氧原子.长方体的8个顶点和中心是钛原子,4个氧原子的位置是A(0.31a,0.31b,0),B(0.69a,0.69b,0),C(0.81a,0,0.5c)和D(0.19a,0.81b,0.5c).中心处钛原子与A处氧原子间的距离叫做键长.当a=b时,试求键长.
金红石(TiO2)的晶胞如图所示,图中色点代表钛原子,黑点代表氧原子.长方体的8个顶点和中心是钛原子,4个氧原子的位置是A(0.31a,0.31b,0),B(0.69a,0.69b,0),C(0.81a,0,0.5c)和D(0.19a,0.81b,0.5c).中心处钛原子与A处氧原子间的距离叫做键长.当a=b时,试求键长.
分析 设长方体的长、宽、高分别是a,b,c.中心处钛原子的坐标是(0.5a,0.5b,0.5c),A(0.31a,0.31b,0),即可求出键长|AE|.
解答 解:设长方体的长、宽、高分别是a,b,c.中心处钛原子的坐标是(0.5a,0.5b,0.5c).
又A(0.31a,0.31b,0),
所以,键长|AE|=$\sqrt{(0.5a-0.31a)^{2}+(0.5b-0.31b)^{2}+(0.5c)^{2}}$=$\sqrt{0.1{9}^{2}{a}^{2}+0.1{9}^{2}{b}^{2}+0.25{c}^{2}}$.
当a=b时,键长|AE|=$\sqrt{0.27{a}^{2}+0.25{c}^{2}}$.
点评 本题考查空间两点间距离的计算,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
7.已知sinα+$\sqrt{3}$cosα=2,则tanα=( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
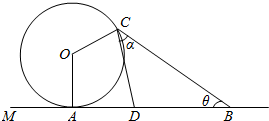 如图,在一条景观道的一端有一个半径为50米的圆形摩天轮O,逆时针15分钟转一圈,从A处进入摩天轮的座舱,OA垂直于地面AM,在距离A处150米处设置了一个望远镜B.
如图,在一条景观道的一端有一个半径为50米的圆形摩天轮O,逆时针15分钟转一圈,从A处进入摩天轮的座舱,OA垂直于地面AM,在距离A处150米处设置了一个望远镜B. 已知抛物线C:y2=2px(p>0)和两条平行线l1,l2,l1过原点O分别交曲线C和C的准线于点P,Q,l2过曲线C的焦点F,交C于点A,B.
已知抛物线C:y2=2px(p>0)和两条平行线l1,l2,l1过原点O分别交曲线C和C的准线于点P,Q,l2过曲线C的焦点F,交C于点A,B.