题目内容
已知函数f(x)=
+
(a,b,λ为实常数).
(1)若λ=-1,a=1.
①当b=-1时,求函数f(x)的图象在点(
,f(
))处的切线方程;
②当b<0时,求函数f(x)在[
,
]上的最大值.
(2)若λ=1,b<a,求证:不等式f(x)≥1的解集构成的区间长度D为定值.
| 1 |
| x-a |
| λ |
| x-b |
(1)若λ=-1,a=1.
①当b=-1时,求函数f(x)的图象在点(
| 2 |
| 2 |
②当b<0时,求函数f(x)在[
| 1 |
| 3 |
| 1 |
| 2 |
(2)若λ=1,b<a,求证:不等式f(x)≥1的解集构成的区间长度D为定值.
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)利用导数的几何意义求得切线斜率,由点斜式写出切线方程,利用导数求出函数在定区间的最大值;
(2)根据一元二次不等式与二次函数的关系,通过分类讨论两根得出结论.
(2)根据一元二次不等式与二次函数的关系,通过分类讨论两根得出结论.
解答:
解 (1)①当b=-1时,f(x)=
-
=
,则f′(x)=
,可得f′(
)=-4
,
又f(
)=2,故所求切线方程为y-2=-4
(x-
),即4
x+y-10=0.
②当λ=-1时,f(x)=
-
,
则f′(x)=-
+
=
.
因为b<0,则b-1<0,且b<
<
故当b<x<
时,f′(x)>0,f(x)在(b,
)上单调递增;
当
<x<
时,f′(x)<0,f(x)在(
,
)单调递减.
(Ⅰ)当
≤
,即b≤-
时,f(x)在[
,
]单调递减,所以[f(x)]max=f(
)=
;
(Ⅱ)当
<
<
,即-
<b<0时,[f(x)]max=f(
)=
.
综上所述,[f(x)]max=
(2)f(x)≥1即
+
≥1.…(*)
①当x<b时,x-a<0,x-b<0,此时解集为空集.
②当a>x>b时,不等式(*)可化为 (x-a)+(x-b)≤(x-a)(x-b),
展开并整理得,x2-(a+b+2)x+(ab+a+b)≥0,
设g (x)=x2-(a+b+2)x+(ab+a+b),
因为△=(a-b)2+4>0,所以g (x)有两不同的零点,设为x1,x2(x1<x2),
又g (a)=b-a<0,g (b)=a-b>0,且b<a,
因此b<x1<a<x2,
所以当a>x>b时,不等式x2-(a+b+2)x+(ab+a+b)≥0的解为b<x≤x1.
③当x>a时,不等式(*)可化为 (x-a)+(x-b)≥(x-a)(x-b),
展开并整理得,x2-(a+b+2)x+(ab+a+b)≤0,
由②知,此时不等式的解为a<x≤x2
综上所述,f(x)≥1的解构成的区间为(b,x1]∪(a,x2],
其长度为(x1-b)+(x2-a)=x1+x2-a-b=a+b+2-a-b=2.
故不等式f(x)≥1的解集构成的区间长度D为定值2.
| 1 |
| x-1 |
| 1 |
| x+1 |
| 2 |
| (x-1)(x+1) |
| -4x |
| (x-1)2(x+1)2 |
| 2 |
| 2 |
又f(
| 2 |
| 2 |
| 2 |
| 2 |
②当λ=-1时,f(x)=
| 1 |
| x-1 |
| 1 |
| x-b |
则f′(x)=-
| 1 |
| (x-1)2 |
| 1 |
| (x-b)2 |
2(b-1)(x-
| ||
| (x-1)2(x-b)2 |
因为b<0,则b-1<0,且b<
| b+1 |
| 2 |
| 1 |
| 2 |
故当b<x<
| b+1 |
| 2 |
| b+1 |
| 2 |
当
| b+1 |
| 2 |
| 1 |
| 2 |
| b+1 |
| 2 |
| 1 |
| 2 |
(Ⅰ)当
| b+1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 9b-9 |
| 2-6b |
(Ⅱ)当
| 1 |
| 3 |
| b+1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| b+1 |
| 2 |
| 4 |
| b-1 |
综上所述,[f(x)]max=
|
(2)f(x)≥1即
| 1 |
| x-a |
| 1 |
| x-b |
①当x<b时,x-a<0,x-b<0,此时解集为空集.
②当a>x>b时,不等式(*)可化为 (x-a)+(x-b)≤(x-a)(x-b),
展开并整理得,x2-(a+b+2)x+(ab+a+b)≥0,
设g (x)=x2-(a+b+2)x+(ab+a+b),
因为△=(a-b)2+4>0,所以g (x)有两不同的零点,设为x1,x2(x1<x2),
又g (a)=b-a<0,g (b)=a-b>0,且b<a,
因此b<x1<a<x2,
所以当a>x>b时,不等式x2-(a+b+2)x+(ab+a+b)≥0的解为b<x≤x1.
③当x>a时,不等式(*)可化为 (x-a)+(x-b)≥(x-a)(x-b),
展开并整理得,x2-(a+b+2)x+(ab+a+b)≤0,
由②知,此时不等式的解为a<x≤x2
综上所述,f(x)≥1的解构成的区间为(b,x1]∪(a,x2],
其长度为(x1-b)+(x2-a)=x1+x2-a-b=a+b+2-a-b=2.
故不等式f(x)≥1的解集构成的区间长度D为定值2.
点评:本题考查了导数的应用、分类讨论思想、解一元二次不等式.其中第(2)问涉及不常考的解一元二次不等式分类讨论问题,注意比较a、b与两根的大小.属难题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
cos
+tan(-
)+sin21π的值为( )
| 9π |
| 4 |
| 7π |
| 6 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
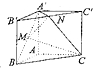 如图,直三角棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=
如图,直三角棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=