题目内容
18.已知6tanαsinα=5,α∈(-$\frac{π}{2}$,0),则sinα的值是-$\frac{\sqrt{5}}{3}$.分析 由已知式子和平方关系可得cosα,由α的范围,求出cosα的值为$\frac{2}{3}$,即可求出sinα的值.
解答 解:∵6tanαsinα=5,
∴6sin2α=5cosα,
∴6cos2α+5cosα-6=0
∵α∈(-$\frac{π}{2}$,0),
∴cosα=$\frac{2}{3}$,
∴sinα=-$\frac{\sqrt{5}}{3}$.
故答案为:-$\frac{\sqrt{5}}{3}$.
点评 此题考查了同角三角函数间的基本关系,熟练掌握公式及基本关系是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.函数f(x)=x2-x-2,x∈[-3,3],那么任取一点x0∈[-3,3],使f(x0)≤0的概率是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{4}{7}$ | D. | $\frac{2}{3}$ |
13.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )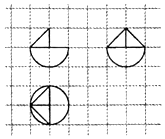

| A. | $\frac{2π+1}{3}$ | B. | $\frac{4π+1}{3}$ | C. | $\frac{2π+3}{3}$ | D. | $\frac{2π+2}{3}$ |
3.已知双曲线${C_1}:\frac{x^2}{2}-{y^2}=1$与双曲线${C_2}:\frac{x^2}{2}-{y^2}=-1$,给出下列说法,其中错误的是( )
| A. | 它们的焦距相等 | B. | 它们的焦点在同一个圆上 | ||
| C. | 它们的渐近线方程相同 | D. | 它们的离心率相等 |
8.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的渐近线将圆x2+y2-2x-4y+4=0平分,则双曲线的离心率为( )
| A. | 3 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
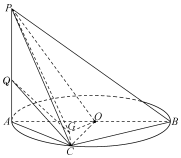 如图,点C在以AB为直径的圆O上,PA垂直与圆O所在平面,G为△AOC的垂心.
如图,点C在以AB为直径的圆O上,PA垂直与圆O所在平面,G为△AOC的垂心.