题目内容
16.已知圆C:(x-1)2+y2=16,F(-1,0),M是圆C上的一个动点,线段MF的垂直平分线与线段MC相交于点P.(Ⅰ)求点P的轨迹方程;
(Ⅱ)记点P的轨迹为C1,A、B是直线x=-2上的两点,满足AF⊥BF,曲线C1与过A,B的两条切线(异于x=-2)交于点Q,求四边形AQBF面积的取值范围.
分析 (I)利用中垂线的性质得出|PF|+|PC|=4,于是P点轨迹为椭圆,根据椭圆定义得出椭圆方程;
(II)设AF的斜率为k,用k表示出A,B的坐标,设过A点的切线斜率为k1,联立方程组得出k1和k的关系,同理得出过B点的切线方程,再联立方程组得出Q点坐标,得出四边形面积关于k的解析式,利用不等式得出面积的范围.
解答  解:(Ⅰ)依题意得圆心C(0,1),半径r=4,
解:(Ⅰ)依题意得圆心C(0,1),半径r=4,
∵线段MF的垂直平分线与线段MC相交于点P,
∴|PF|+|PC|=|PM|+|PC|=CM=4>|CF|=2.
∴点P的轨迹方程是以C,F为焦点,长轴长为4的椭圆,
即a=2,c=1,则b=22-1=3,
∴P的轨迹方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(Ⅱ)依题意,直线AF斜率存在且不为零,设为y=k(x+1),
令x=-2得A(-2,-k),同理B(-2,$\frac{1}{k}$).
设过点A的切线为y=k1(x+2)-k,代入$\frac{x^2}{4}+\frac{y^2}{3}=1$
得$(3+4{k_1}^2){x^2}+8{k_1}(2{k_1}$$-k)x+4{(2{k_1}-k)^2}-12=0$x+4[(2k1-k)2-3]=0.
由$△=64{k_1}^2{(2{k_1}-k)^2}-16(3+4{k_1}^2)$$[{{{(2{k_1}-k)}^2}-3}]=0$,解得${k_1}=\frac{{{k^2}-3}}{4k}$,
同理k2=$\frac{(-\frac{1}{k})^{2}-3}{4•(-\frac{1}{k})}$=$\frac{{3{k^2}-1}}{4k}$.
联立方程组:$\left\{{\begin{array}{l}{y=\frac{{{k^2}-3}}{4k}(x+2)-k}\\{y=\frac{{3{k^2}-1}}{4k}(x+2)+\frac{1}{k}}\end{array}}\right.$,解得x=-4.
∴${S_{AQBF}}=\frac{1}{2}|{AB}||{{x_F}-{x_Q}}|$=$\frac{3}{2}|{k+\frac{1}{k}}|≥3$,当且仅当k=±1时等号成立,
∴四边形AQBF面积的取值范围是[3,+∞).
点评 本题考查了椭圆的定义,直线与椭圆的位置关系,属于中档题.

 优等生题库系列答案
优等生题库系列答案| A. | -3 | B. | 3 | C. | -5 | D. | 5 |
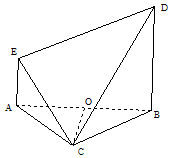 如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.