题目内容

15．已知集合$A=\left\{{\left.x\right|y=\frac{1}{{\sqrt{-3x-{x^2}}}}}\right\}$，集合$B=\left\{{\left.x\right|\frac{1}{8}＜{2^x}＜2}\right\}$．
（1）求A∩B；
（2）若集合C={x|2a≤x≤a+1}，且（A∩B）?C，求实数a的取值范围．

分析 （1）先把集合A，B解出来，即可求A∩B；
（2）对集合C进行讨论，然后求解．

解答 解：（1）解A=（-3，0），B=（-3，1），
所以A∩B=（-3，0）
（2）若C=∅时，2a＞a+1，即a＞1；
  若C≠∅时，$\left\{\begin{array}{l}{2a≤a+1}\\{2a＞-3}\\{a+1＜0}\end{array}\right.$，解得-$\frac{3}{2}＜a＜-1$     
  综上：$-\frac{3}{2}＜a＜-1$或a＞1．

点评 本题主要考查集合的自交并的运算，属于基础题．

练习册系列答案
相关题目
9．过点（4，6）且与圆（x-2）2+（y-3）2=4相切的直线方程是5x-12y+77=0或x=4．
6．圆C的圆心C（1，2），该圆上一个动点P到直线l：x+y+1=0的距离的最小值为$\sqrt{2}$．
（1）求圆C的标准方程；
（2）过点C作两条互相垂直的直线与直线l交于A，B两个点，求|AB|的最小值．
3．设函数f（x）=$\frac{2}{3}$+$\frac{1}{x}$（x＞0），数列{an}满足a1=1，an=f（$\frac{1}{{a}_{n-1}}$），n∈N*，且n≥2．
（1）求数列{an}的通项公式；
（2）对n∈N*，设Sn=$\frac{1}{a_1a_2}$+$\frac{1}{a_2a_3}$+$\frac{1}{a_3a_4}$+…+$\frac{1}{a_na_{n+1}}$，若Sn≥3t恒成立，求实数t的取值范围．
10．计算：
（1）$\root{4}{{{{（3-π）}^4}}}+{（{0.008}）^{-\frac{1}{3}}}-{（{0.25}）^{\frac{1}{2}}}×{（{\frac{1}{{\sqrt{2}}}}）^{-4}}$；
（2）$\frac{1}{2}lg\frac{32}{49}-\frac{4}{3}lg\sqrt{8}+lg\sqrt{245}+{2^{1+{{log}_2}3}}$．
20．已知数列{an}的前n项和为Sn，满足a1=2，Sn+2=2an，n∈N*
（1）求an；
（2）求证：$\frac{a_1}{{（{{a_1}+1}）（{{a_2}+1}）}}+\frac{a_2}{{（{{a_2}+1}）（{{a_3}+1}）}}+…+\frac{a_n}{{（{{a_n}+1}）（{{a_{n+1}}+1}）}}＜\frac{1}{3}$．
7．若函数$f（x）=|sinx+\frac{2}{3+sinx}+t|（x，t∈R）$最大值记为g（t），则函数g（t）的最小值为$\frac{3}{4}$．
4．顶点在原点、坐标轴为对称轴的抛物线，过点（-1，2），则它的方程是（　　）
A．y=2x2或y2=-4xB．y2=-4x或x2=2yC．x2=-$\frac{1}{2}$yD．y2=-4x
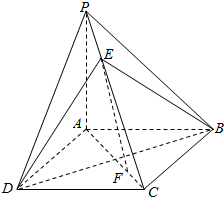5．如图，四棱锥P-ABCD中，底面ABCD是正方形，PA⊥平面ABCD，点E、F在PC、AC上，PE=$\frac{1}{4}$PC．
（I）若EF∥平面PBD，求的$\frac{AF}{AC}$的值；
（II）若PA=AB，三棱锥C-BDE的体积为8，求正方形ABCD的边长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网