题目内容
5.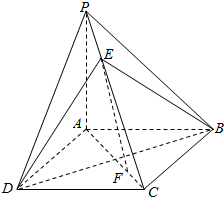 如图,四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,点E、F在PC、AC上,PE=$\frac{1}{4}$PC.
如图,四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,点E、F在PC、AC上,PE=$\frac{1}{4}$PC.(I)若EF∥平面PBD,求的$\frac{AF}{AC}$的值;
(II)若PA=AB,三棱锥C-BDE的体积为8,求正方形ABCD的边长.
分析 (1)设AB,BD交于点G,连结PG,利用线面平行的性质可得EF∥PG,在利用相似三角形得出$\frac{CF}{FG}$,再根据G是AC中点推出$\frac{AF}{AC}$.
(2)根据体积列出方程解出底面边长.
解答 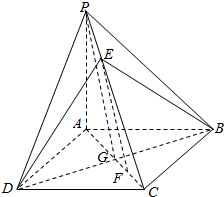 解:(1)设AB,BD交于点G,连结PG,∵EF∥平面PBD,EF?平面PAC,平面PAC∩平面PBD=PG,
解:(1)设AB,BD交于点G,连结PG,∵EF∥平面PBD,EF?平面PAC,平面PAC∩平面PBD=PG,
∴EF∥PG,∴△CEF∽△CPG,∴$\frac{CF}{CG}=\frac{CE}{PC}$=$\frac{3}{4}$.
∵底面ABCD是正方形,∴AG=CG,∴$\frac{CF}{AC}=\frac{3}{8}$.∴$\frac{AF}{AC}$=$\frac{5}{8}$.
(2)设底面ABCD的边长为x.则S△BCD=$\frac{{x}^{2}}{2}$,PA=x,
∴V棱锥C-BDE=$\frac{1}{3}$×S△BCD×$\frac{3}{4}$x=$\frac{{x}^{3}}{8}$=8,∴x=4.
∴正方形ABCD的边长是4.
点评 本题考查了线面平行的性质,相似三角形,棱锥的体积,属于中档题.

练习册系列答案
相关题目
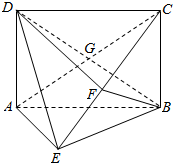 如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC和BD交于点G.
如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC和BD交于点G.