题目内容
设圆C的方程为x2+y2-2x-2y-2=0,直线l的方程为(m+1)x-my-1=0,圆C被直线l截得的弦长等于( )
| A、4 | ||
B、2
| ||
| C、2 | ||
| D、与m有关 |
考点:直线与圆相交的性质
专题:直线与圆
分析:由圆心C(1,1)到直线l:(m+1)x-my-1=0的距离d=0,得到圆C被直线l截得的弦长为圆C的直径.
解答:
解:∵圆C的方程为x2+y2-2x-2y-2=0,
∴圆C的圆心C(1,1),半径r=
=2,
圆心C(1,1)到直线l:(m+1)x-my-1=0的距离:
d=
=0,
∴圆C被直线l截得的弦长为圆C的直径,其值为4.
故选:A.
∴圆C的圆心C(1,1),半径r=
| 1 |
| 2 |
| 4+4-4×(-2) |
圆心C(1,1)到直线l:(m+1)x-my-1=0的距离:
d=
| |m+1-m-1| | ||
|
∴圆C被直线l截得的弦长为圆C的直径,其值为4.
故选:A.
点评:本题考查圆的弦长的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
已知向量
=(1,2),
=(-2,t),
∥
,则t=( )
| m |
| n |
| m |
| n |
| A、-4 | B、-2 | C、0 | D、1 |
已知
,
是夹角为60°的两个单位向量,则
=2
+
与
=-3
+2
的夹角的正弦值是( )
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
若a=0.63,b=log30.2,c=30.6,则( )
| A、c>a>b |
| B、a>c>b |
| C、c>b>a |
| D、b>c>a |
若抛物线y2=4x的焦点是F,准线是l,则经过点F、M(4,4)且与l相切的圆共有( )
| A、4个 | B、2个 | C、1个 | D、0个 |
有一种细菌和一种病毒,每个细菌在每秒钟杀死一个病毒的同时将自身分裂为3个,现在有一个这样的细菌和110个这样的病毒,问细菌将病毒全部杀死至少需要( )
| A、4秒钟 | B、5秒钟 |
| C、6秒钟 | D、7秒钟 |
若四点A(5,0),B(-1,0),C(a,2),D(3,-2)共圆,则正实数a=( )
| A、2 | B、3 | C、4 | D、5 |
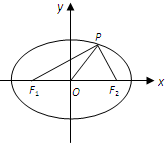 如图,F1,F2分别为椭圆
如图,F1,F2分别为椭圆