题目内容
11.已知常数ω>0,f(x)=-1+2$\sqrt{3}$sinωxcosωx+2cos2ωx图象的对称中心得到对称轴的距离的最小值为$\frac{π}{4}$,若f(x0)=$\frac{6}{5}$,$\frac{π}{4}$≤x0≤$\frac{π}{2}$,则cos2x0=( )| A. | $\frac{3+2\sqrt{3}}{10}$ | B. | $\frac{3-2\sqrt{2}}{10}$ | C. | $\frac{3+4\sqrt{3}}{10}$ | D. | $\frac{3-4\sqrt{3}}{10}$ |
分析 将函数f(x)化简成只有一个函数名,对称中心得到对称轴的距离的最小值为$\frac{π}{4}$,可得T=π.根据f(x0)=$\frac{6}{5}$,$\frac{π}{4}$≤x0≤$\frac{π}{2}$,求出x0,可得cos2x0的值.
解答 解:由f(x)=-1+2$\sqrt{3}$sinωxcosωx+2cos2ωx,
化简可得:f(x)=$\sqrt{3}$sin2ωx+cos2ωx=2sin(2ωx+$\frac{π}{6}$)
∵对称中心得到对称轴的距离的最小值为$\frac{π}{4}$,
∴T=π.
由$T=\frac{2π}{2ω}=π$,
可得:ω=1.
f(x0)=$\frac{6}{5}$,即2sin(2x0+$\frac{π}{6}$)=$\frac{6}{5}$
∵$\frac{π}{4}$≤x0≤$\frac{π}{2}$,
∴$\frac{2π}{3}$≤2x0+$\frac{π}{6}$≤$\frac{7π}{6}$
∴sin(2x0+$\frac{π}{6}$)=$\frac{3}{5}$>0
∴cos(2x0+$\frac{π}{6}$)=$-\frac{4}{5}$.
那么:cos2x0=cos(2x0+$\frac{π}{6}$-$\frac{π}{6}$)=cos(2x0+$\frac{π}{6}$)cos$\frac{π}{6}$+sin(2x0+$\frac{π}{6}$)sin$\frac{π}{6}$=$\frac{3-4\sqrt{3}}{10}$
故选D
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.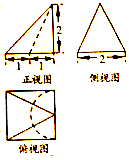 某零件的三视图如图所示,则该零件的体积为( )
某零件的三视图如图所示,则该零件的体积为( )
 某零件的三视图如图所示,则该零件的体积为( )
某零件的三视图如图所示,则该零件的体积为( )| A. | $\frac{7}{3}$ | B. | $\frac{8-π}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{7-π}{3}$ |
2.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x-1}-2,x≥1}\\{{2}^{1-x}-2,x<1}\end{array}\right.$,则不等式f(x-1)≤0的解集为( )
| A. | {x|0≤x≤2} | B. | {x|0≤x≤3} | C. | {x|1≤x≤2} | D. | {x|1≤x≤3} |
19.设a、b都是不等于1的正数,则“a>b>1”是“loga3<logb3”的( )条件.
| A. | 充要 | B. | 充分非必要 | ||
| C. | 必要非充分 | D. | 既非充分也非必要 |
6.已知$\overrightarrow{a}$、$\overrightarrow{b}$是平面向量,如果|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=4,|$\overrightarrow{a}$+$\overrightarrow{b}$|=2,那么|$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | $\sqrt{46}$ | B. | 7 | C. | 5 | D. | $\sqrt{21}$ |
3.已知函数f(x)=alnx-ax-3(a∈R).若函数y=f(x)的图象在点(2,f(2))处切线的倾斜角为$\frac{π}{4}$,对于任意t∈[1,2]函数g(x)=x3+x2[f′(x)+$\frac{m}{2}$]在区间(t,3)上总不是单调函数,则实数 m 的取值范围是( )
| A. | ?(-∞,-5)? | B. | ?(-$\frac{37}{3}$,-5)? | C. | (-9,+∞)?? | D. | (-$\frac{37}{3}$,-9)? |