题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x-1}-2,x≥1}\\{{2}^{1-x}-2,x<1}\end{array}\right.$,则不等式f(x-1)≤0的解集为( )| A. | {x|0≤x≤2} | B. | {x|0≤x≤3} | C. | {x|1≤x≤2} | D. | {x|1≤x≤3} |
分析 由已知中函数f(x)=$\left\{\begin{array}{l}{{2}^{x-1}-2,x≥1}\\{{2}^{1-x}-2,x<1}\end{array}\right.$是一个分段函数,故可以将不等式f(x-1)≤0分类讨论,分x-1≥1和x-1<1两种情况,分别进行讨论,综合讨论结果,即可得到答案.
解答 解:当x-1≥1,即x≥2时,f(x-1)≤0?2x-2-2≤0,解得x≤3,∴2≤x≤3;
当x-1<1,即x<2时,f(x-1)≤0?22-x-2≤0,解得x≥1,∴1≤x<2.
综上,不等式f(x-1)≤0的解集为{x|1≤x≤3}.
故选:D.
点评 本题考查的知识点是分段函数的解析式,及不等式的解法,其中根据分段函数分段处理的原则,对不等式f(x+2)≤3的变形进行分类讨论,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知四棱锥P-ABCD的顶点都在球O的球面上,底面ABCD是矩形,平面PAD⊥底面ABCD,△PAD为正三角形,AB=2AD=4,则球O的表面积为( )
| A. | $\frac{56π}{3}$ | B. | $\frac{64π}{3}$ | C. | 24π | D. | $\frac{80π}{3}$ |
10.设$f(x)=\left\{\begin{array}{l}x+4,x≤-2或x≥3\\{x^2}-1,-2<x<3\end{array}\right.$,若函数y=f(x)+k的图象与x轴恰有三个不同交点,则k的取值范围是( )
| A. | (-2,1) | B. | [0,1] | C. | [-2,0) | D. | [-2,1) |
17.已知甲、乙两组数据的茎叶图如图所示,若它们的中位数相同,则甲组数据的平均数为( )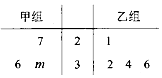

| A. | 32 | B. | 33 | C. | 34 | D. | 35 |
7.某校开展“翻转合作学习法”教学实验,经过一年的实践后,对“翻转班”和“对照班”的全部220名学生的数学学习情况进行测试,按照大于或等于120分为“成绩优秀”,120分以下为“成绩一般”统计,得到如下的2×2列联表.
(Ⅰ)根据上面的列联表判断,能否在犯错误的概率不超过0.001的前提下认为“成绩优秀与翻转合作学习法”有关;
(Ⅱ)为了交流学习方法,从这次测试数学成绩优秀的学生中,用分层抽样方法抽出6名学生,再从这6名学生中抽3名出来交流学习方法,求至少抽到一名“对照班”学生交流的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$:
| 成绩优秀 | 成绩一般 | 合计 | |
| 对照班 | 20 | 90 | 110 |
| 翻转班 | 40 | 70 | 110 |
| 合计 | 60 | 160 | 220 |
(Ⅱ)为了交流学习方法,从这次测试数学成绩优秀的学生中,用分层抽样方法抽出6名学生,再从这6名学生中抽3名出来交流学习方法,求至少抽到一名“对照班”学生交流的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
14.执行如图所示的程序框图,若输入n=10,则输出S=( )
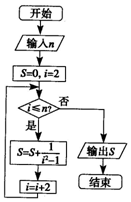

| A. | $\frac{4}{9}$ | B. | $\frac{5}{11}$ | C. | $\frac{6}{13}$ | D. | $\frac{36}{55}$ |
11.已知常数ω>0,f(x)=-1+2$\sqrt{3}$sinωxcosωx+2cos2ωx图象的对称中心得到对称轴的距离的最小值为$\frac{π}{4}$,若f(x0)=$\frac{6}{5}$,$\frac{π}{4}$≤x0≤$\frac{π}{2}$,则cos2x0=( )
| A. | $\frac{3+2\sqrt{3}}{10}$ | B. | $\frac{3-2\sqrt{2}}{10}$ | C. | $\frac{3+4\sqrt{3}}{10}$ | D. | $\frac{3-4\sqrt{3}}{10}$ |
12.已知a>0,且a≠1,若ab>1,则( )
| A. | ab>b | B. | ab<b | C. | a>b | D. | a<b |