若所有形如3a+$\sqrt{2}$b的数组成集合A.判断6-2$\sqrt{2}$是不是集合A中的元素．题目和参考答案——青夏教育精英家教网——

题目内容

3．若所有形如3a+$\sqrt{2}$b（a∈Z，b∈Z）的数组成集合A，判断6-2$\sqrt{2}$是不是集合A中的元素．

分析根据元素与集合的关系进行判断

解答解：所有形如3a+$\sqrt{2}$b（a∈Z，b∈Z）的数组成集合A，
当a=2，b=-2时，可得集合A中的元素为：6-2$\sqrt{2}$．
∴6-2$\sqrt{2}$是集合A中的元素．

点评本题主要考查元素与集合的关系，属于基础题．

练习册系列答案

金太阳全A加系列答案

创新导学案新课标寒假假期自主学习训练系列答案

超能学典暑假接力棒江苏凤凰少年儿童出版社系列答案

暑假提高班系列答案

完美假期暑假作业系列答案

快乐假期高考状元假期学习方案暑假系列答案

豫欣图书自主课堂系列答案

假期伙伴寒假大连理工大学出版社系列答案

鑫宇文化新课标快乐假期暑假系列答案

学霸错题笔记系列答案

相关题目

11．已知常数ω＞0，f（x）=-1+2$\sqrt{3}$sinωxcosωx+2cos²ωx图象的对称中心得到对称轴的距离的最小值为$\frac{π}{4}$，若f（x₀）=$\frac{6}{5}$，$\frac{π}{4}$≤x₀≤$\frac{π}{2}$，则cos2x₀=（　　）

$\frac{3+2\sqrt{3}}{10}$

$\frac{3-2\sqrt{2}}{10}$

$\frac{3+4\sqrt{3}}{10}$

$\frac{3-4\sqrt{3}}{10}$

12．已知a＞0，且a≠1，若a^b＞1，则（　　）

9．已知$\overrightarrow{a}$=（-1，3）与$\overrightarrow{b}$=（0，6），求5$\overrightarrow{a}$-2$\overrightarrow{b}$的坐标，并求|5$\overrightarrow{a}$-2$\overrightarrow{b}$|．

16．已知函数f（x）=2sin（x+$\frac{π}{6}$）-2cosx，x∈[$\frac{π}{2}$，π]．
（1）若sinx=$\frac{4}{5}$，求函数f（x）的值；
（2）求函数f（x）的值域和对称轴．

8．△ABC中，2$\overrightarrow{OA}$+3$\overrightarrow{OB}$+4$\overrightarrow{OC}$=$\overrightarrow{0}$，求$\frac{{S}_{△OBC}}{{S}_{△ABC}}$．

15．已知在△ABC中，AB=AC=6，∠BAC=120°，D是BC边上靠近点B的四等分点，F是AC边的中点，若点G是△ABC的重心，则$\overrightarrow{GD}$•$\overrightarrow{AF}$=-$\frac{21}{4}$．

12．椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个焦点与它的一个顶点的连线构成等腰直角三角形，直线x+y=0与以椭圆C的右顶点为圆心，以2b为半径的圆相交所得的弦长为2$\sqrt{3}$．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）设过椭圆C右焦点F₂的直线l与椭圆交于点P、Q，若以OP，OQ为邻边的平行四边形是矩形，求满足该条件的直线l的方程．

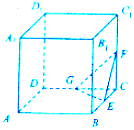如图所示，正方体ABCD-A₁B₁C₁D₁的棱长为1，E，F，G分别是棱BC，CC₁，CD的中点，平面α过点B₁且与平面EFG平行，则平面α被该正方体外接球所截得的截面圆的面积为为$\frac{2}{3}π$．