题目内容
已知p(x)=x,fn(x)=(1+x)n.
(1)若g(x)=p(1)f5(x)+p(2)f6(x)+p(3)f7(x),求g(x)的展开式中x5的系数;
(2)证明:C
+2C
+3C
+…+nC
=
C
(m,n∈N*).
(1)若g(x)=p(1)f5(x)+p(2)f6(x)+p(3)f7(x),求g(x)的展开式中x5的系数;
(2)证明:C
m m |
m m+1 |
m m+2 |
m m+n-1 |
| (m+1)n+1 |
| m+2 |
m+1 m+n |
考点:二项式定理的应用
专题:二项式定理
分析:(1)利用二项式定理中展开式特点,发现g(x)的展开式中x5的系数为
+2
+3
,计算可得;
(2)由(1)可知等式的左边为函数h(x)=(1+x)m+2(1+x)m+1+3(1+x)m+2+…+n(1+x)m+n的展开式的xm的系数,利用错位相减法中午等比数列的求和形式解答.
| C | 5 5 |
| C | 5 6 |
| C | 5 7 |
(2)由(1)可知等式的左边为函数h(x)=(1+x)m+2(1+x)m+1+3(1+x)m+2+…+n(1+x)m+n的展开式的xm的系数,利用错位相减法中午等比数列的求和形式解答.
解答:
解:(1)由已知得g(x)=1(1+x)5+2(1+x)6+3(1+x)7,
∴g(x)的展开式中x5的系数为
+2
+3
=76;
(2)由(1)知C
+2C
+3C
+…+nC
为函数h(x)=(1+x)m+2(1+x)m+1+3(1+x)m+2+…+n(1+x)m+n的展开式的xm的系数,
又(1+x)h(x)=(1+x)m+1+2(1+x)m+2+3(1+x)m+3+…+n(1+x)m+n+1,
两式相减得-xh(x)=(1+x)m+(1+x)m+1+(1+x)m+2+…+(1+x)m+n+1-n(1+x)m+n
=
-n(1+x)m+n,
∴x2h(x)=(1+x)m-(1+x)m+n+nx(1+x)m+n,
∴h(x)展开式中xm的系数等于x2h(x)展开式中xm+2的系数
为-
+n
=
,
∴C
+2C
+3C
+…+nC
=
C
(m,n∈N*).
∴g(x)的展开式中x5的系数为
| C | 5 5 |
| C | 5 6 |
| C | 5 7 |
(2)由(1)知C
m m |
m m+1 |
m m+2 |
m m+n-1 |
又(1+x)h(x)=(1+x)m+1+2(1+x)m+2+3(1+x)m+3+…+n(1+x)m+n+1,
两式相减得-xh(x)=(1+x)m+(1+x)m+1+(1+x)m+2+…+(1+x)m+n+1-n(1+x)m+n
=
| (1+x)m[1-(1+x)n] |
| 1-(1+x) |
∴x2h(x)=(1+x)m-(1+x)m+n+nx(1+x)m+n,
∴h(x)展开式中xm的系数等于x2h(x)展开式中xm+2的系数
为-
| C | m+2 m+n |
| C | m+1 m+n |
| (m+1)n+1 |
| m+2 |
| C | m+1 m+n |
∴C
m m |
m m+1 |
m m+2 |
m m+n-1 |
| (m+1)n+1 |
| m+2 |
m+1 m+n |
点评:本题考查了二项式定理的运用以及错位相减法求数列的和的问题.

练习册系列答案
相关题目
在数列{an},a1=1,an+1=
(n∈N*),则a5=( )
| 2an |
| an+2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设f0(x)=cosx,且对任意的n∈N,都有 fn+1(x)=fn′(x),则f2013(x)=( )
| A、cosx | B、sinx |
| C、-sinx | D、-cosx |
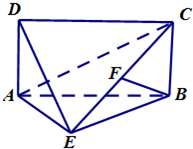 如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.