题目内容
4个男同学和3个女同学站成一排
(1)甲乙两同学之间必须恰有3人,有多少种不同的排法?
(2)甲乙两人相邻,但都不与丙相邻,有多少种不同的排法?
(3)女同学从左到右按高矮顺序排,有多少种不同的排法?(3个女生身高互不相等)
(1)甲乙两同学之间必须恰有3人,有多少种不同的排法?
(2)甲乙两人相邻,但都不与丙相邻,有多少种不同的排法?
(3)女同学从左到右按高矮顺序排,有多少种不同的排法?(3个女生身高互不相等)
考点:计数原理的应用
专题:应用题,排列组合
分析:(1)因为要求甲乙之间恰有3人,可以先选3人放入甲乙之间,再把这5人看做一个整体,与剩余的2个元素进行全排列,注意甲乙之间还有一个排列;
(2)先排甲、乙和丙3人以外的其他4人,由于甲乙要相邻,故再把甲、乙排好,最后把甲、乙排好的这个整体与丙分别插入原先排好的4人的空档中;
(3)因为女同学从左往右按从高到低排,所以3个同学的顺序是确定的,只需先不考虑女同学的顺序,把7人进行全排列,再除以女同学的一个全排列即可得到结果.
(2)先排甲、乙和丙3人以外的其他4人,由于甲乙要相邻,故再把甲、乙排好,最后把甲、乙排好的这个整体与丙分别插入原先排好的4人的空档中;
(3)因为女同学从左往右按从高到低排,所以3个同学的顺序是确定的,只需先不考虑女同学的顺序,把7人进行全排列,再除以女同学的一个全排列即可得到结果.
解答:
解:(1)甲乙两人先排好,有
种排法,再从余下的5人中选3人排在甲乙两人中间,有
种排法;这时把已排好的5人看作一个整体,与最后剩下得2人再排,又有
种排法这时共有
=720种不同排法.
(2)先排甲、乙和丙3人以外的其他4人有
种排法,由于甲乙要相邻,故再把甲、乙排好,有
种排法,最后把甲、乙排好的这个整体与丙分别插入原先排好的4人的空档中,有
种排法,共有
=960(种)不同排法.
(3)从7个位置中选出4个位置把男生排好,有
种排法;然后再在余下的3个空位置中排女生,由于女生要按高矮排列,故仅有一种排法,共有
=840种不同排法.
| A | 2 2 |
| A | 3 3 |
| A | 3 3 |
| A | 2 2 |
| A | 3 3 |
| A | 3 3 |
(2)先排甲、乙和丙3人以外的其他4人有
| A | 4 4 |
| A | 2 2 |
| A | 2 5 |
| A | 4 4 |
| A | 2 2 |
| A | 2 5 |
(3)从7个位置中选出4个位置把男生排好,有
| A | 4 7 |
| A | 4 7 |
点评:本题主要考查排列组合的实际应用,本题涉及到相邻问题,顺序确定问题,本题解题的关键是对于有限制元素的问题的解法,本题是一个中档题目

练习册系列答案
相关题目
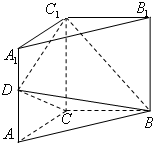 如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,F为双曲线
如图,F为双曲线