题目内容
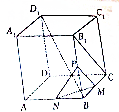 如图,在棱长为2的正方体ABCD一A1B1C1D1中,M为BC的中点,N为AB的中点,P为BB1的中点.
如图,在棱长为2的正方体ABCD一A1B1C1D1中,M为BC的中点,N为AB的中点,P为BB1的中点.(1)求证:BD1⊥B1C;
(2)求证:BD1⊥平面MNP.
考点:直线与平面垂直的判定,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)利用正方体的性质得到AB⊥平面BCC1B1,B1C⊥BC1,只要判断B1C⊥平面ABC1D1即可;
(2)连接BC1,欲证BD1⊥平面MNP,根据直线与平面垂直的判定定理可知只需证BD1与平面MNP内两相交直线垂直,而BD1⊥PM,而BD1⊥MN,MN∩PM=M,满足定理条件;
(2)连接BC1,欲证BD1⊥平面MNP,根据直线与平面垂直的判定定理可知只需证BD1与平面MNP内两相交直线垂直,而BD1⊥PM,而BD1⊥MN,MN∩PM=M,满足定理条件;
解答:
证明:(1)连接BC1,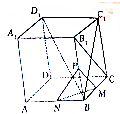
∵几何体为正方体,∴AB⊥平面BCC1B1,B1C⊥BC1
∴AB⊥B1C,
∴B1C⊥平面ABC1D1,
∴B1C⊥BD1即BD1⊥B1C;
(2)由正方体的性质得BC1是BD1在平面BCC1B1内的射影,且B1C⊥BC1,
∴BD1⊥B1C,
∵M为BC的中点,N为AB的中点,P为BB1的中点.
∴B1C∥PM,∴BD1⊥PM,而BD1⊥MN
又MN∩PM=M,
∴BD1⊥平面MNP.

∵几何体为正方体,∴AB⊥平面BCC1B1,B1C⊥BC1
∴AB⊥B1C,
∴B1C⊥平面ABC1D1,
∴B1C⊥BD1即BD1⊥B1C;
(2)由正方体的性质得BC1是BD1在平面BCC1B1内的射影,且B1C⊥BC1,
∴BD1⊥B1C,
∵M为BC的中点,N为AB的中点,P为BB1的中点.
∴B1C∥PM,∴BD1⊥PM,而BD1⊥MN
又MN∩PM=M,
∴BD1⊥平面MNP.
点评:本题主要考查了直线与平面垂直的判定,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=
,则函数g(x)=f(x)-x在区间[-5,5]上的零点之和为( )
|
| A、15 | B、16 | C、30 | D、32 |
过抛物线y2=2px的焦点F作直线交抛物线于M,N两点,弦MN的垂直平分线交x轴于点H,若|MN|=40,则|HF|=( )
| A、14 | B、16 | C、18 | D、20 |
| cos200 |
| sin200 |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
 如图,正方体ABCD-A1B1C1D1的棱长为a,求:
如图,正方体ABCD-A1B1C1D1的棱长为a,求: