过抛物线y2=2px的焦点F作直线交抛物线于M.N两点.弦MN的垂直平分线交x轴于点H.若|MN|=40.则|HF|=( ) A.14B.16C.18D.20 题目和参考答案——青夏教育精英家教网—

题目内容

过抛物线y²=2px的焦点F作直线交抛物线于M，N两点，弦MN的垂直平分线交x轴于点H，若|MN|=40，则|HF|=（　　）

A、14

B、16

C、18

D、20

考点：抛物线的简单性质

专题：计算题,圆锥曲线的定义、性质与方程

分析：先求MN的垂直平分线，求出MN的垂直平分线交x轴于H的坐标，进而求得|HF|=

|MN|，即可得出结论．

解答： 解：设M（x₁，y₁），N（x₂，y₂），弦MN的中点为M′（x₀，y₀），则kMN=

∴MN的垂直平分线为y-y₀=-

（x-x₀）
令y=0，则x_H=x₀+p
∴|HF|=x₀+

∵|MN|=x₁+x₂+p=2x₀+p
∴|HF|=

|MN|=20，
故选：D．

点评：本题以抛物线方程为载体，考查抛物线的性质，考查学生的计算能力，比较基础．

练习册系列答案

若等腰梯形ABCD中，AB∥CD，AB=3，BC=

设函数f（x）是R上的单调函数，且满足：对任意x，y∈R，都有f（x+y）=f（x）+f（y）且f（1）=2，问：实数k为何值时，存在t＞2，使得f（klog₂t）+f[（log₂t）²-log₂t-2]＜0？

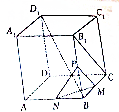如图，在棱长为2的正方体ABCD一A₁B₁C₁D₁中，M为BC的中点，N为AB的中点，P为BB₁的中点．
（1）求证：BD₁⊥B₁C；
（2）求证：BD₁⊥平面MNP．

对于（1+2x）ⁿ（n∈N^*）的展开式，当n≥8时，若从二项式系数中任取一项，使这个二项式系数小于

的概率大于0.7，求n的取值范围．

质点运动规律为s=t²-3，则在时间（3，3+△t）中相应的平均速度为（　　）

（a，b，c∈R且为常数），函数f（x）在x=0处取得极值1．
（1）求实数a，b的值；
（2）若函数y=f（x）在区间（-∞，2]上的最大值为1，求实数c的取值范围．

已知2cosα+sinα=

．
（Ⅰ）求sinα的值；
（Ⅱ）若cos（α+β）=

，α，β均为锐角，求
（i）cosβ的值；（ii）2α+β的值．

试题分类