题目内容
已知函数f(x)=
,则函数g(x)=f(x)-x在区间[-5,5]上的零点之和为( )
|
| A、15 | B、16 | C、30 | D、32 |
考点:分段函数的应用,函数零点的判定定理
专题:函数的性质及应用
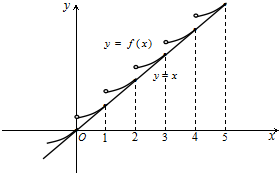
分析:对函数f(x)分“x≤0”“0<x≤1”“1<x≤2”“2<x≤3”“3<x≤4”“4<x≤5”进行讨论,分别写出f(x)的表达式,并作出f(x)的图象,通过函数f(x)与直线y=x的交点情况,探求方程f(x)=x的实根,即得函数g(x)=f(x)-x的所有零点,从而求得所有零点之和.
解答:
解:根据函数f(x)=
,
(1)当x≤0时,f(x)=2x-1,在函数g(x)=f(x)-x=2x-1-x中,
由g(0)=0知,g(x)有零点x0=0;
(2)当0<x≤1时,-1<x-1≤0,f(x)=f(x-1)+1=2x-1-1+1=2x-1,
由g(1)=f(1)-1=21-1-1=0,得g(x)有零点x1=1;
(3)当1<x≤2时,-1<x-2≤0,f(x)=f(x-1)+1=[f(x-2)+1]+1=2x-2+1,
由g(2)=f(2)-2=[22-2+1]-2=0,得g(x)有零点x2=2;
(4)当2<x≤3时,-1<x-3≤0,同理得f(x)=2x-3+2,
由g(3)=f(3)-3=[23-3+2]-3=0,得g(x)有零点x3=3;
(5)当3<x≤4时,-1<x-4≤0,得f(x)=2x-4+3,
由g(4)=f(4)-4=[24-4+3]-4=0,得g(x)有零点x4=4;
(6)当4<x≤5时,-1<x-5≤0,得f(x)=2x-5+4,
由g(5)=f(5)-5=[25-5+4]-5=0,得g(x)有零点x5=5.
作出函数f(x)及y=x在[-5,5]的图象,两图象共6个公共点,如右图所示.
所以g(x)=f(x)-x在区间[-5,5]上的零点之和为0+1+2+3+4+5=15.
故答案为:A.
|

(1)当x≤0时,f(x)=2x-1,在函数g(x)=f(x)-x=2x-1-x中,
由g(0)=0知,g(x)有零点x0=0;
(2)当0<x≤1时,-1<x-1≤0,f(x)=f(x-1)+1=2x-1-1+1=2x-1,
由g(1)=f(1)-1=21-1-1=0,得g(x)有零点x1=1;
(3)当1<x≤2时,-1<x-2≤0,f(x)=f(x-1)+1=[f(x-2)+1]+1=2x-2+1,
由g(2)=f(2)-2=[22-2+1]-2=0,得g(x)有零点x2=2;
(4)当2<x≤3时,-1<x-3≤0,同理得f(x)=2x-3+2,
由g(3)=f(3)-3=[23-3+2]-3=0,得g(x)有零点x3=3;
(5)当3<x≤4时,-1<x-4≤0,得f(x)=2x-4+3,
由g(4)=f(4)-4=[24-4+3]-4=0,得g(x)有零点x4=4;
(6)当4<x≤5时,-1<x-5≤0,得f(x)=2x-5+4,
由g(5)=f(5)-5=[25-5+4]-5=0,得g(x)有零点x5=5.
作出函数f(x)及y=x在[-5,5]的图象,两图象共6个公共点,如右图所示.
所以g(x)=f(x)-x在区间[-5,5]上的零点之和为0+1+2+3+4+5=15.
故答案为:A.
点评:本题考查了分段函数的图象,函数零点的判断与求解,关键是将函数的零点问题转化为对应方程的实根问题,并结合图象进行处理.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
质点运动规律为s=t2-3,则在时间(3,3+△t)中相应的平均速度为( )
| A、3 | B、6 | C、9 | D、12 |
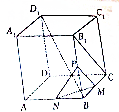 如图,在棱长为2的正方体ABCD一A1B1C1D1中,M为BC的中点,N为AB的中点,P为BB1的中点.
如图,在棱长为2的正方体ABCD一A1B1C1D1中,M为BC的中点,N为AB的中点,P为BB1的中点.