题目内容
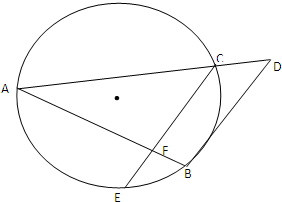如图已知AB和AC是圆的两条弦．过点B作圆的切线与AC的延长线相交于点D，过点C作BD的平行线与圆相交于点E，与AB相交于点F，AF=3，FB=1，CD=| 4 |
| 3 |
考点：与圆有关的比例线段
专题：立体几何
分析：由已知得△ACF∽△ABD，从而
=
，
=
=
，进而得到AC=4，由切割线定理得BD=
，从而CF=2，由相交弦定理得AF•FB=EF•CF，由此能求出EF．
| AF |
| FB |
| AC |
| CD |
| CF |
| BD |
| AF |
| AB |
| 3 |
| 4 |
| 8 |
| 3 |
解答：
解：∵过点C作BD的平行线与圆相交于点E，与AB相交于点F，
∴△ACF∽△ABD，∴
=
，
=
=
，
∵AF=3，FB=1，CD=
，
∴AC=
=
=4，
∵过点B作圆的切线与AC的延长线相交于点D，
∴由切割线定理得BD2=CD•CA=
×(
+4)=
，∴BD=
，
∴CF=
BD=2，
由相交弦定理得AF•FB=EF•CF，
∴EF=
=
=
．
故答案为：
．
∴△ACF∽△ABD，∴
| AF |
| FB |
| AC |
| CD |
| CF |
| BD |
| AF |
| AB |
| 3 |
| 4 |
∵AF=3，FB=1，CD=
| 4 |
| 3 |
∴AC=
| AF×CD |
| FB |
3×
| ||
| 1 |
∵过点B作圆的切线与AC的延长线相交于点D，
∴由切割线定理得BD2=CD•CA=
| 4 |
| 3 |
| 4 |
| 3 |
| 64 |
| 9 |
| 8 |
| 3 |
∴CF=
| 3 |
| 4 |
由相交弦定理得AF•FB=EF•CF，
∴EF=
| AF×FB |
| CF |
| 3×1 |
| 2 |
| 3 |
| 2 |
故答案为：
| 3 |
| 2 |
点评：本试题主要考查了平面几何中直线与圆的位置关系，相交弦定理，切割线定理，相似三角形的概念、判定与性质．
练习册系列答案
优学名师名题系列答案
相关题目
设
Ak=A1∪A2∪A3∪…An，n∈N*，设集合Ak={y|y=
，
≤x≤1，k=2，3，…，2015}，则
Ak=（ ）
| ||
| k=3 |
| kx+1 | ||
|
| 1 |
| k |
| ||
| k=2 |
| A、∅ | ||||
B、[2，
| ||||
| C、{2} | ||||
D、[2，
|
下列函数中，与函数y=
+
有相同定义域的是（ ）
| 1 | ||
|
| 1 | ||
|
| A、f（x）=lnx+1g（1-x） | ||||
B、f（x）=
| ||||
C、f（x）=
| ||||
| D、f（x）=ex |
若函数f（x）=
在[2，+∞）上有意义，则实数a的取值范围为（ ）
| ax-2 |
| A、a=1 | B、a＞1 |
| C、a≥1 | D、a≥0 |
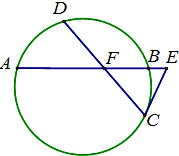如图，已知图中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF=CF=