题目内容
若函数f（x）=
在[2，+∞）上有意义，则实数a的取值范围为（ ）
| ax-2 |
| A、a=1 | B、a＞1 |
| C、a≥1 | D、a≥0 |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件，解参数即可．
解答：
解：∵函数f（x）=
在[2，+∞）上有意义，
∴ax-2≥0在[2，+∞）上恒成立，
即a≥
在[2，+∞）恒成立，
∵0＜
≤1，
∴a≥1，
故选：C．
| ax-2 |
∴ax-2≥0在[2，+∞）上恒成立，
即a≥
| 2 |
| x |
∵0＜
| 2 |
| x |
∴a≥1，
故选：C．
点评：本题主要考查函数恒成立问题，根据函数的定义域是解决本题的关键．
练习册系列答案
相关题目
已知复数z满足（1+
i）z=1+i，则|z|=（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
复数Z=-
+
i，则Z3=（ ）
| 1 |
| 2 |
| ||
| 2 |
| A、-1 | B、1 |
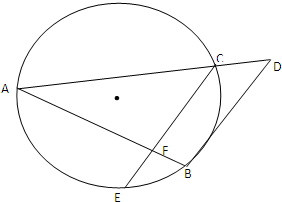如图已知AB和AC是圆的两条弦．过点B作圆的切线与AC的延长线相交于点D，过点C作BD的平行线与圆相交于点E，与AB相交于点F，AF=3，FB=1，CD=
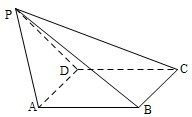如图，已知四棱锥P-ABCD，PB⊥AD侧面PAD为边长等于2的正三角形，底面ABCD为菱形，侧面PAD与底面ABCD所成的二面角为120°．