题目内容
设
Ak=A1∪A2∪A3∪…An,n∈N*,设集合Ak={y|y=
,
≤x≤1,k=2,3,…,2015},则
Ak=( )
| ||
| k=3 |
| kx+1 | ||
|
| 1 |
| k |
| ||
| k=2 |
| A、∅ | ||||
B、[2,
| ||||
| C、{2} | ||||
D、[2,
|
考点:并集及其运算
专题:探究型,函数的性质及应用,集合
分析:根据基本不等式和函数的单调性求出集合Ak,再由题意表示出
Ak,利用并集的运算求出即可.
| ||
| k=2 |
解答:
解:因为,
≤x≤1,k=2,3,…,2015,
所以
=
+
≥2
=2,
当且仅当
=
时,即x=
时取等号,
所以函数y=
在[
,1]上的最小值是2,
由对号函数的单调性知,函数y=
在[
,1]上单调递增,
所以当x=1时取到最大值
=
,即集合Ak=[2,
](k≥2),
因为
Ak=A1∪A2∪A3∪…An,n∈N*,且Ak={2},
所以
Ak=A1∪A2∪A3∪…A2015={2}∪[2,
]∪…∪[2,
]
=[2,
],
故选:D.
| 1 |
| k |
所以
| kx+1 | ||
|
| kx |
| 1 | ||
|
|
当且仅当
| kx |
| 1 | ||
|
| 1 |
| k |
所以函数y=
| kx+1 | ||
|
| 1 |
| k |
由对号函数的单调性知,函数y=
| kx+1 | ||
|
| 1 |
| k |
所以当x=1时取到最大值
| k+1 | ||
|
(k+1)
| ||
| k |
(k+1)
| ||
| k |
因为
| ||
| k=3 |
所以
| ||
| k=2 |
3
| ||
| 2 |
2016
| ||
| 2015 |
=[2,
2016
| ||
| 2015 |
故选:D.
点评:本题是探究型的题目,考查基本不等式和函数的单调性在求函数的最值中的应用,以及并集的运算.

练习册系列答案
相关题目
以正方体ABCD-A1B1C1D1的棱AB、AD、AA1所在的直线为坐标轴建立空间直角坐标系,且正方体的棱长为一个单位长度,则棱CC1中点坐标为( )
A、(
| ||||
B、(1,
| ||||
C、(1,1,
| ||||
D、(
|
“a>b”是“ac2>bc2”的( )
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
已知{an}是等比数列,a2=1,a3=
,则公比q为( )
| 1 |
| 4 |
A、
| ||
B、-
| ||
| C、4 | ||
| D、-4 |

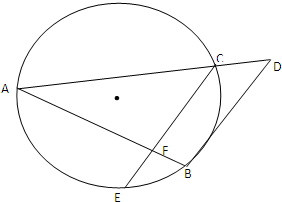 如图已知AB和AC是圆的两条弦.过点B作圆的切线与AC的延长线相交于点D,过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,CD=
如图已知AB和AC是圆的两条弦.过点B作圆的切线与AC的延长线相交于点D,过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,CD=