题目内容
已知实数a,b,c成等差数列,点P(-3,0)在动直线ax+by+c=0(a,b不同时为零)上的射影点为M,若点N的坐标为(2,3),则线段MN长度的最大值是 .
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:实数a,b,c成等差数列,可得2b=a+c,于是动直线l:ax+by+c=0(a,b不同时为零)化为:ax+
y+c=0,即a(2x+y)+c(y+2)=0,利用直线系可得:动直线l过定点:Q(1,-2).因此点M在以PQ为直径的圆上,利用中点坐标公式可得:圆心为线段PQ的中点:C(-1,-1),半径r.则线段MN长度的最大值=|CN|+r.
| a+c |
| 2 |
解答:
解:∵实数a,b,c成等差数列,
∴2b=a+c,
∴动直线l:ax+by+c=0(a,b不同时为零)化为:ax+
y+c=0,变形为a(2x+y)+c(y+2)=0,
令
,解得
.
∴动直线l过定点:Q(1,-2).
∴点M在以PQ为直径的圆上,
圆心为线段PQ的中点:C(-1,-1),半径r=
=
.
∴线段MN长度的最大值=|CN|+r=
+
=5+
.
故答案为:5+
.
∴2b=a+c,
∴动直线l:ax+by+c=0(a,b不同时为零)化为:ax+
| a+c |
| 2 |
令
|
|
∴动直线l过定点:Q(1,-2).
∴点M在以PQ为直径的圆上,
圆心为线段PQ的中点:C(-1,-1),半径r=
| 22+1 |
| 5 |
∴线段MN长度的最大值=|CN|+r=
| 32+42 |
| 5 |
| 5 |
故答案为:5+
| 5 |
点评:本题综合考查了直线系、等差数列的性质、圆的性质、点与圆的位置关系、两点之间的距离公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知3+sin2β+2t>(2
+
t)sin(β+
)+
对于β∈[0,
]恒成立,则t的取值范围是( )
| 2 |
| 2 |
| π |
| 4 |
2
| ||
cos(
|
| π |
| 2 |
| A、t>4 | B、t>3 |
| C、t>2 | D、t≥-2 |
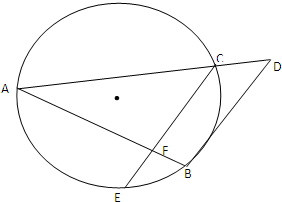 如图已知AB和AC是圆的两条弦.过点B作圆的切线与AC的延长线相交于点D,过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,CD=
如图已知AB和AC是圆的两条弦.过点B作圆的切线与AC的延长线相交于点D,过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,CD=