题目内容
已知函数f(x)为偶凼数,且对任意x∈R满足f(1+x)=f(1-x),若当x∈[0,1]时,f(x)=x2,求x∈[2015,2016]时f(x)的表达式.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:由题意求出函数的周期,转化求x∈[1,2)的函数的解析式
解答:
解:函数f(x)为偶凼数,且满足且对任意x∈R满足f(1+x)=f(1-x),
令x=x+1,则f(2+x)=f(1-1-x)=f(-x)=f(x),
∴函数的周期为2,f(2015)=f(2×1007+1)=f(1),f(2016)=f(2×1007+2)=f(2),
∵x∈[0,1]时,f(x)=x2,
∴x∈[-1,0]时,f(x)=x2,
当x∈[1,2)时,只要把f(x)的图象x∈[-1,0]时向右平移2个单即可
∴f(x)=(x-2)2,x∈[1,2)
∴f(x)=(x-2)2,x∈[2015,2016]
令x=x+1,则f(2+x)=f(1-1-x)=f(-x)=f(x),
∴函数的周期为2,f(2015)=f(2×1007+1)=f(1),f(2016)=f(2×1007+2)=f(2),
∵x∈[0,1]时,f(x)=x2,
∴x∈[-1,0]时,f(x)=x2,
当x∈[1,2)时,只要把f(x)的图象x∈[-1,0]时向右平移2个单即可
∴f(x)=(x-2)2,x∈[1,2)
∴f(x)=(x-2)2,x∈[2015,2016]
点评:本题考查了函数的奇偶性和周期性以及函数的解析式的求法,属于基础题

练习册系列答案
相关题目
如图,已知四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,则下列命题中错误的是( )
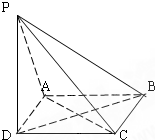

| A、过BD且与PC平行的平面交PA于M点,则M为PA的中点 |
| B、过AC且与PB垂直的平面交PB于N点,则N为PB的中点 |
| C、过AD且与PC垂直的平面交PC于H点,则H为PC的中点 |
| D、过P、B、C的平面与平面PAD的交线为直线l,则l∥AD |
已知椭圆C:
+x2=1,过点P(
,
)的直线与椭圆C相交于A,B两点,且弦AB被点P平分,则直线AB的方程为( )
| y2 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、9x-y-4=0 |
| B、9x+y-5=0 |
| C、4x+2y-3=0 |
| D、4x-2y-1=0 |
已知3+sin2β+2t>(2
+
t)sin(β+
)+
对于β∈[0,
]恒成立,则t的取值范围是( )
| 2 |
| 2 |
| π |
| 4 |
2
| ||
cos(
|
| π |
| 2 |
| A、t>4 | B、t>3 |
| C、t>2 | D、t≥-2 |
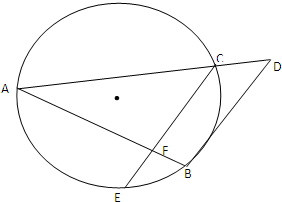 如图已知AB和AC是圆的两条弦.过点B作圆的切线与AC的延长线相交于点D,过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,CD=
如图已知AB和AC是圆的两条弦.过点B作圆的切线与AC的延长线相交于点D,过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,CD=