题目内容
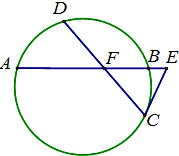 如图,已知图中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=
如图,已知图中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=| 2 |
| ||
| 2 |
考点:与圆有关的比例线段
专题:立体几何
分析:由相交弦定理得DF•FC=AF•BF,由此解得AF=2,BF=1,AB=3,由切割线定理得CE2=BE•AE,由此能求出BE的长.
解答:
解:∵两条弦AB与CD相交于点F,E是AB延长线上一点,
∴DF•FC=AF•BF,
∵DF=CF=
,AF=2BF,
∴2BF2=2,解得AF=2,BF=1,AB=3,
∵CE与圆相切,且CE=
,
∴CE2=BE•AE,∴(
)2=BE(3+BE),
解得BE=
,或BE=-
(舍).
故答案为:
.
∴DF•FC=AF•BF,
∵DF=CF=
| 2 |
∴2BF2=2,解得AF=2,BF=1,AB=3,
∵CE与圆相切,且CE=
| ||
| 2 |
∴CE2=BE•AE,∴(
| ||
| 2 |
解得BE=
| 1 |
| 2 |
| 7 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查与圆有关的线段长的求法,是中档题,解题时要注意相交弦定理和切割线定理的合理运用.

练习册系列答案
相关题目
已知{an}是等比数列,a2=1,a3=
,则公比q为( )
| 1 |
| 4 |
A、
| ||
B、-
| ||
| C、4 | ||
| D、-4 |
复数
=( )
| 1+2i |
| 1-i |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知集合A={x|x2-2x≤0,x∈R},集合B={x||x|≤1,x∈R},则A∩B为( )
| A、{x|0≤x≤2} |
| B、{x|1≤x≤2} |
| C、{x|-1≤x≤2} |
| D、{x|0≤x≤1} |
如图,已知四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,则下列命题中错误的是( )
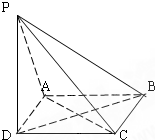

| A、过BD且与PC平行的平面交PA于M点,则M为PA的中点 |
| B、过AC且与PB垂直的平面交PB于N点,则N为PB的中点 |
| C、过AD且与PC垂直的平面交PC于H点,则H为PC的中点 |
| D、过P、B、C的平面与平面PAD的交线为直线l,则l∥AD |
已知椭圆C:
+x2=1,过点P(
,
)的直线与椭圆C相交于A,B两点,且弦AB被点P平分,则直线AB的方程为( )
| y2 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、9x-y-4=0 |
| B、9x+y-5=0 |
| C、4x+2y-3=0 |
| D、4x-2y-1=0 |
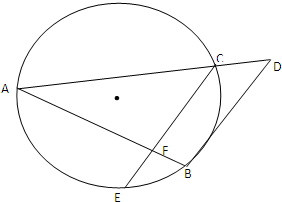 如图已知AB和AC是圆的两条弦.过点B作圆的切线与AC的延长线相交于点D,过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,CD=
如图已知AB和AC是圆的两条弦.过点B作圆的切线与AC的延长线相交于点D,过点C作BD的平行线与圆相交于点E,与AB相交于点F,AF=3,FB=1,CD=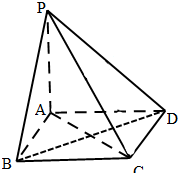 已知四棱锥P-ABCD中,PA⊥面ABCD,四边形ABCD是正方形,且AB=a,PA=
已知四棱锥P-ABCD中,PA⊥面ABCD,四边形ABCD是正方形,且AB=a,PA=