题目内容
9．下面的函数中，周期为π的奇函数是（ ）| A． | y=tan2x | B． | y=cos2x | C． | y=sin2x | D． | $y=sin\frac{x}{2}$ |
分析 利用三角函数的奇偶性与周期性进行判断即可．
解答 解：对于A，y=tan2x的周期为T=$\frac{π}{2}$，不合题意；
对于B，y=cos2x是偶函数，不合题意；
对于C，y=sin2x的周期为T=π，且是奇函数，满足题意；
对于D，y=sin$\frac{x}{2}$的周期为T=4π，不合题意．
故选：C．
点评 本题考查了函数的奇偶性与周期性的应用问题，是基础题目．
练习册系列答案
相关题目
17．已知f（x）是定义在[0，+∞）上单调递增的函数，则满足$f（{2x-1}）＜f（{\frac{1}{3}}）$的x取值范围是（ ）
| A． | $（{\frac{1}{2}\;，\;\;\frac{2}{3}}）$ | B． | $（{-∞\;，\;\;\frac{2}{3}}）$ | C． | $[{\frac{1}{2}\;，\;\;\frac{2}{3}}）$ | D． | $（{-∞\;，\;\;\frac{2}{3}}]$ |
1．点P（2，4）关于直线x+y+1=0的对称点的坐标为（ ）
| A． | （5，-3） | B． | （3，-5） | C． | （-5，3） | D． | （-5，-3） |
18．
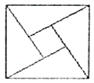2002年8月，在北京召开的国际数学家大会会标如图所示，它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形，若直角三角形中较小的锐角为θ，大正方形的面积是25，小正方形的面积是1，则cos2θ的值等于（ ）
2002年8月，在北京召开的国际数学家大会会标如图所示，它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形，若直角三角形中较小的锐角为θ，大正方形的面积是25，小正方形的面积是1，则cos2θ的值等于（ ）| A． | 1 | B． | $-\frac{24}{25}$ | C． | $\frac{7}{25}$ | D． | -$\frac{7}{25}$ |