题目内容
18.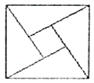 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是25,小正方形的面积是1,则cos2θ的值等于( )
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是25,小正方形的面积是1,则cos2θ的值等于( )| A. | 1 | B. | $-\frac{24}{25}$ | C. | $\frac{7}{25}$ | D. | -$\frac{7}{25}$ |
分析 根据题意可知每个直角三角形的长直角边为cosθ,短直角边为sinθ,小正方形的边长为cosθ-sinθ,先利用小正方形的面积求得∴(cosθ-sinθ)2的值,根据θ为直角三角形中较小的锐角,判断出cosθ>sinθ 求得cosθ-sinθ的值,进而求得2cosθsinθ利用配方法求得(cosθ+sinθ)2的进而求得cosθ+sinθ,利用二倍角公式把cos2θ=cos2θ-sin2θ 展开后,把cosθ+sinθ和cosθ-sinθ的值代入即可求得答案.
解答 解:依题意可知拼图中的每个直角三角形的长直角边为cosθ,短直角边为sinθ,小正方形的边长为cosθ-sinθ,
∵小正方形的面积是$\frac{1}{25}$,∴(cosθ-sinθ)2=$\frac{1}{25}$.
又θ为直角三角形中较小的锐角,∴cosθ>sinθ,∴cosθ-sinθ=$\frac{1}{5}$.
又∵(cosθ-sinθ)2=1-2sinθcosθ=$\frac{1}{25}$,∴2cosθsinθ=$\frac{24}{25}$,
∴1+2sinθcosθ=$\frac{49}{25}$,即(cosθ+sinθ)2=$\frac{49}{25}$,∴cosθ+sinθ=$\frac{7}{5}$.
∴cos2θ=cos2θ-sin2θ=(cosθ+sinθ)(cosθ-sinθ)=$\frac{7}{5}$•$\frac{1}{5}$=$\frac{7}{25}$,
故选:C.
点评 本题主要考查了三角函数的化简求值,同角三角函数的基本关系.考查了学生综合分析推理和基本的运算能力,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
9.下面的函数中,周期为π的奇函数是( )
| A. | y=tan2x | B. | y=cos2x | C. | y=sin2x | D. | $y=sin\frac{x}{2}$ |




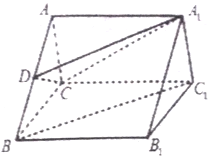 如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,过A1C作平面A1CD平行于BC1,交AB于D点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,过A1C作平面A1CD平行于BC1,交AB于D点.