题目内容
14．△ABC中，a、b、c分别为角A、B、C的对边，$a=6，b=5\sqrt{2}$，$cosA=\frac{4}{5}$，则∠B=45o或135o．分析 由已知利用同角三角函数基本关系式可求sinA的值，进而利用正弦定理可得sinB的值，结合范围B∈（0°，180°），可求B的值．
解答 解：∵$cosA=\frac{4}{5}$，可得：sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{3}{5}$，
∴由正弦定理可得：sinB=$\frac{bsinA}{a}$=$\frac{5\sqrt{2}×\frac{3}{5}}{6}$=$\frac{\sqrt{2}}{2}$，
∵B∈（0°，180°），
∴B=45°或135o．
故答案为：45o或135o．
点评 本题主要考查了同角三角函数基本关系式，正弦定理，特殊角的三角函数值在解三角形中的应用，考查了转化思想，属于基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
5．设a，b∈R，则“a＞b”是“a＞|b|”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
9．下面的函数中，周期为π的奇函数是（ ）
| A． | y=tan2x | B． | y=cos2x | C． | y=sin2x | D． | $y=sin\frac{x}{2}$ |
19．
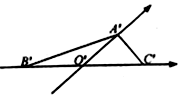已知水平放置的△A BC是按“斜二测画法”得到如图所示的直观图，其中 B'O'=C'O'=1，${A}'{O}'=\frac{{\sqrt{3}}}{2}$，那么对于原△ABC则有（ ）
已知水平放置的△A BC是按“斜二测画法”得到如图所示的直观图，其中 B'O'=C'O'=1，${A}'{O}'=\frac{{\sqrt{3}}}{2}$，那么对于原△ABC则有（ ）| A． | AB=BC | B． | AB=BC，且AB⊥BC | C． | AB⊥BC | D． | AB=AC，且AB⊥AC |
