题目内容
17.已知f(x)是定义在[0,+∞)上单调递增的函数,则满足$f({2x-1})<f({\frac{1}{3}})$的x取值范围是( )| A. | $({\frac{1}{2}\;,\;\;\frac{2}{3}})$ | B. | $({-∞\;,\;\;\frac{2}{3}})$ | C. | $[{\frac{1}{2}\;,\;\;\frac{2}{3}})$ | D. | $({-∞\;,\;\;\frac{2}{3}}]$ |
分析 根据函数单调性的性质,建立不等式关系进行求解即可.
解答 解:∵f(x)是定义在[0,+∞)上单调递增的函数,
∴不等式$f({2x-1})<f({\frac{1}{3}})$等价为0≤2x-1<$\frac{1}{3}$,即$\frac{1}{2}$≤x<$\frac{2}{3}$,
即不等式的解集为$[{\frac{1}{2}\;,\;\;\frac{2}{3}})$,
故选:C.
点评 本题主要考查不等式的求解,根据函数单调性的性质建立不等式关系是解决本题的关键.

练习册系列答案
相关题目
5.设a,b∈R,则“a>b”是“a>|b|”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.下面的函数中,周期为π的奇函数是( )
| A. | y=tan2x | B. | y=cos2x | C. | y=sin2x | D. | $y=sin\frac{x}{2}$ |




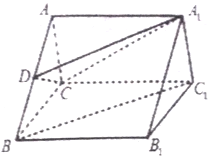 如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,过A1C作平面A1CD平行于BC1,交AB于D点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,过A1C作平面A1CD平行于BC1,交AB于D点.