题目内容
已知向量
=(2sinx,2sinx),
=(cosx,-sinx),求函数f(x)=
•
+1.
(1)如果f(x)=
,求sin4x的值.
(2)如果x∈(0,
),求f(x)的取值范围.
| a |
| b |
| a |
| b |
(1)如果f(x)=
| 1 |
| 2 |
(2)如果x∈(0,
| π |
| 2 |
考点:平面向量数量积的运算,三角函数中的恒等变换应用
专题:三角函数的求值,平面向量及应用
分析:计算向量的数量积,利用二倍角.两角和的正弦函数化简函数f(x)的表达式,得到一个角的一个三角函数的形式;
(1)借助诱导公式和二倍角公式,求出sin4x的值.
(2)先求出2x+
的范围,再根据正弦函数的单调性,求出函数的值域.
(1)借助诱导公式和二倍角公式,求出sin4x的值.
(2)先求出2x+
| π |
| 4 |
解答:
解:∵
=(2sinx,2sinx),
=(cosx,-sinx),
∴f(x)=
•
+1=2sinxcosx-2sin2x+1=sin2x+co2x=
sin(2x+
),
(1)∵f(x)=
,
∴
sin(2x+
)=
,
∴sin(2x+
)=
,
∴sin4x=-cos(4x+
)=-cos2(2x+
)=-[1-2sin2(2x+
)]=-1+2×
=0,
(2)∵x∈(0,
),
∴2x+
∈(
,
),
∴-
<sin(2x+
)<1,
∴-1<
sin(2x+
)<
,
∴f(x)的取值范围(-1,
).
| a |
| b |
∴f(x)=
| a |
| b |
| 2 |
| π |
| 4 |
(1)∵f(x)=
| 1 |
| 2 |
∴
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴sin(2x+
| π |
| 4 |
| ||
| 2 |
∴sin4x=-cos(4x+
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
(2)∵x∈(0,
| π |
| 2 |
∴2x+
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
∴-
| ||
| 2 |
| π |
| 4 |
∴-1<
| 2 |
| π |
| 4 |
| 2 |
∴f(x)的取值范围(-1,
| 2 |
点评:本题考查了三角函数的二倍角公式,三角函数的化简,向量的数量积,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
等比数列{an}的前n项和为Sn,若S2014=3(a1+a3+a5+…+a2013),a1a2a3=8,则log2a2014的值为( )
| A、2012 | B、2013 |
| C、2014 | D、无法确定 |
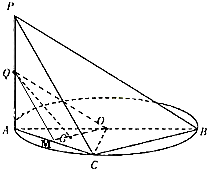 如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.
如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.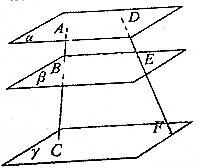 如图,直线AC、DF被三个平行平面α、β、γ所截:
如图,直线AC、DF被三个平行平面α、β、γ所截: