题目内容
已知函数f(x)=log2
,求证:f(x1)+f(x2)=f(
).
| 1+x |
| 1-x |
| x1+x2 |
| 1+x1x2 |
考点:对数的运算性质
专题:函数的性质及应用
分析:直接把要证的等式两边代入函数f(x)=log2
,整理后得答案.
| 1+x |
| 1-x |
解答:
证明:∵f(x)=log2
,
∴f(x1)+f(x2)=log2
+log2
=log2
.
f(
)=log2
=log2
=log2
.
∴f(x1)+f(x2)=f(
).
| 1+x |
| 1-x |
∴f(x1)+f(x2)=log2
| 1+x1 |
| 1-x1 |
| 1+x2 |
| 1-x2 |
| (1+x1)(1+x2) |
| (1-x1)(1-x2) |
f(
| x1+x2 |
| 1+x1x2 |
1+
| ||
1-
|
| 1+x1+x2+x1x2 |
| 1-x1-x2+x1x2 |
| (1+x1)(1+x2) |
| (1-x1)(1-x2) |
∴f(x1)+f(x2)=f(
| x1+x2 |
| 1+x1x2 |
点评:本题考查了对数的运算性质,考查了计算能力,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合A={1,2},B={1},则“x∈A”是“x∈B”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设偶函数f(x)的定义域为R,当x∈[0,+∞)时f(x)是增函数,则f(-2),f(π),f(-3)的大小关系是( )
| A、f(π)<f(-2)<f(-3) |
| B、f(π)<f(-3)<f(-2) |
| C、f(π)>f(-2)>f(-3) |
| D、f(π)>f(-3)>f(-2) |
命题“?x>1,log2x>0”的否定形式是( )
| A、?x0>1,log2x≤0 |
| B、?x0≤1,log2x≤0 |
| C、?x>1,log2x≤0 |
| D、?x≤1,log2x>0 |
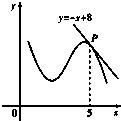 如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=( )
如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=( )| A、2 | ||
| B、1 | ||
C、
| ||
| D、0 |
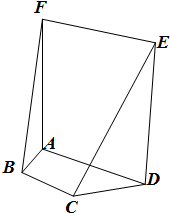 如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=2
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=2