题目内容
20．已知四边形ABCD为梯形，AB∥CD，l为空间一直线，则“l垂直于两腰AD，BC”是“l垂直于两底AB，CD”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 四边形ABCD为梯形，AB∥CD，l为空间一直线，则“l垂直于两腰AD，BC”，又AD与BC相交．∴l⊥平面ABCD⇒l垂直于两底AB，CD，反之不成立．即可判断出结论．
解答 解：四边形ABCD为梯形，AB∥CD，l为空间一直线，则“l垂直于两腰AD，BC”，又AD与BC相交．
∴l⊥平面ABCD⇒l垂直于两底AB，CD，反之不成立．
∴“l垂直于两腰AD，BC”是“l垂直于两底AB，CD”的充分不必要条件．
故选：A．
点评 本题考查了空间线面垂直的判定与性质定理、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
8．
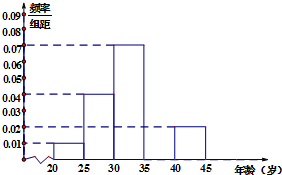当今，手机已经成为人们不可或缺的交流工具，人们常常把喜欢玩手机的人冠上了名号“低头族”，手机已经严重影响了人们的生活，一媒体为调查市民对低头族的认识，从某社区的500名市民中，随机抽取n名市民，按年龄情况进行统计的得到频率分布表和频率分布直方图如下：
（1）求出表中的a，b，n的值，并补全频率分布直方图；
（2）媒体记者为了做好调查工作，决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访，再从抽出的这20名中年龄在[30，40）的选取2名担任主要发言人．记这2名主要发言人年龄在[35，40）的人数为ξ，求ξ的分布列及数学期望．
当今，手机已经成为人们不可或缺的交流工具，人们常常把喜欢玩手机的人冠上了名号“低头族”，手机已经严重影响了人们的生活，一媒体为调查市民对低头族的认识，从某社区的500名市民中，随机抽取n名市民，按年龄情况进行统计的得到频率分布表和频率分布直方图如下：| 组数 | 分组（单位：岁） | 频数 | 频率 |
| 1 | [20，25） | 5 | 0.05 |
| 2 | [25，30） | 20 | 0.20 |
| 3 | [30，35） | a | 0.35 |
| 4 | [35，40） | 30 | b |
| 5 | [40，45] | 10 | 0.10 |
| 合计 | n | 1.00 | |
（2）媒体记者为了做好调查工作，决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访，再从抽出的这20名中年龄在[30，40）的选取2名担任主要发言人．记这2名主要发言人年龄在[35，40）的人数为ξ，求ξ的分布列及数学期望．
15．当今，手机已经成为人们不可或缺的交流工具，人们常常把喜欢玩手机的人冠上了名号“低头族”，手机已经严重影响了人们的生活，一媒体为调查市民对低头族的认识，从某社区的500名市民中，随机抽取n名市民，按年龄情况进行统计的得到频率分布表和频率分布直方图如下：
（1）求出表中的a，b的值，并补全频率分布直方图；
（2）媒体记者为了做好调查工作，决定在第2，4，5组中用分层抽样的方法抽取6名市民进行问卷调查，再从这6名市民中随机抽取2名接受电视采访，求第2组至少有一名接受电视采访的概率？
当今，手机已经成为人们不可或缺的交流工具，人们常常把喜欢玩手机的人冠上了名号“低头族”，手机已经严重影响了人们的生活，一媒体为调查市民对低头族的认识，从某社区的500名市民中，随机抽取n名市民，按年龄情况进行统计的得到频率分布表和频率分布直方图如下：| 组数 | 分组（单位：岁） | 频数 | 频率 |
| 1 | [20，25） | 5 | 0.05 |
| 2 | [25，30） | 20 | 0.20 |
| 3 | [30，35） | a | 0.35 |
| 4 | [35，40） | 30 | b |
| 5 | [40，45] | 10 | 0.10 |
| 合计 | n | 1.00 | |
（2）媒体记者为了做好调查工作，决定在第2，4，5组中用分层抽样的方法抽取6名市民进行问卷调查，再从这6名市民中随机抽取2名接受电视采访，求第2组至少有一名接受电视采访的概率？
如图1，在边长为2的菱形ABCD中，∠BAD=60°，将△BCD沿对角线BD折起到△B'CD的位置，使平面BC'D⊥平面ABD，E是BD的中点，FA⊥平面ABD，且FA=2$\sqrt{3}$，如图2．