题目内容
9.以坐标原点为对称中心,两坐标轴为对称轴的双曲线C的一条渐近线倾斜角为$\frac{π}{3}$,则双曲线C的离心率为2或$\frac{2\sqrt{3}}{3}$.分析 由双曲线的焦点位置,分类讨论:$\frac{b}{a}$=tan$\frac{π}{3}$=$\sqrt{3}$,或$\frac{a}{b}$=tan$\frac{π}{3}$=$\sqrt{3}$,根据c2=a2+b2即可求得即可求得a和c的关系,根据双曲线的离心率公式,即可求得双曲线C的离心率.
解答 解:∵以坐标原点为对称中心,两坐标轴为对称轴的双曲线C的一条渐近线的倾斜角为$\frac{π}{3}$,
当双曲线的焦点在x轴上时,$\frac{b}{a}$=tan$\frac{π}{3}$=$\sqrt{3}$,
当双曲线的焦点在y轴上时,$\frac{a}{b}$=tan$\frac{π}{3}$=$\sqrt{3}$,
当$\frac{b}{a}$=$\sqrt{3}$时,b=$\sqrt{3}$a,
c2=a2+3a2=4a2,c=2a,
此时e=$\frac{c}{a}$=2,
当$\frac{a}{b}$=$\sqrt{3}$,时,b=$\frac{\sqrt{3}}{3}$a,c2=a2+b2=a2+$\frac{1}{3}$a2=$\frac{4}{3}$a2,c=$\frac{2\sqrt{3}}{3}$a,
此时e=$\frac{c}{a}$=$\frac{2\sqrt{3}}{3}$,
∴双曲线C的离心率2或$\frac{2\sqrt{3}}{3}$,
故答案为:2或$\frac{2\sqrt{3}}{3}$,
点评 本题考查双曲线的渐近线方程及双曲线的离心率公式,考查分类讨论思想,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
20.已知四边形ABCD为梯形,AB∥CD,l为空间一直线,则“l垂直于两腰AD,BC”是“l垂直于两底AB,CD”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.设等差数列{an}的前n项和为Sn,若S9=54,则a1+a5+a9=( )
| A. | 9 | B. | 15 | C. | 18 | D. | 36 |
4.设集合M={x|-2<x<3}N={-2,-1,0,1}},则M∩N=( )
| A. | {-2,-1,0} | B. | {0,1,2} | C. | {-1,0,1} | D. | {-2,-1,0,1} |
1.cos70°sin50°-cos200°sin40°的值为( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
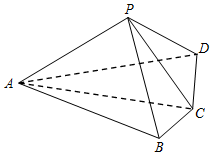 如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.
如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.