��Ŀ����
10�� ��ͼ1���ڱ߳�Ϊ2������ABCD�У���BAD=60�㣬����BCD�ضԽ���BD����B'CD��λ�ã�ʹƽ��BC'D��ƽ��ABD��E��BD���е㣬FA��ƽ��ABD����FA=2$\sqrt{3}$����ͼ2��
��ͼ1���ڱ߳�Ϊ2������ABCD�У���BAD=60�㣬����BCD�ضԽ���BD����B'CD��λ�ã�ʹƽ��BC'D��ƽ��ABD��E��BD���е㣬FA��ƽ��ABD����FA=2$\sqrt{3}$����ͼ2����1����֤��FA��ƽ��BC'D��
��2����ƽ��ABD��ƽ��FBC'���ɽǵ�����ֵ��
��3�����߶�AD���Ƿ����һ��M��ʹ��C'M��ƽ��FBC�������ڣ���$\frac{AM}{AD}$��ֵ���������ڣ�˵�����ɣ�
���� ��1��������ɵ�C��E��BD����ƽ��BC'D��ƽ��ABD����ƽ��BC'D��ƽ��ABD=BD���������洹ֱ�����ʿɵ�C��E��ABD�������֪�ɵ�FA��C��E��������ƽ�е��ж��ɵ�FA��ƽ��BC'D��
��2����DB����ֱ��Ϊx�ᣬAE����ֱ��Ϊy�ᣬEC������ֱ��Ϊz�Ὠ���ռ�ֱ������ϵ��������õ�����꣬���ƽ��FBC����ƽ��ABD��һ�����������������������ɽǵ�����ֵ�ɵ�ƽ��ABD��ƽ��FBC'���ɽǵ�����ֵ��
��3���������߶�AD�ϴ���M��x��y��z����ʹ��C'M��ƽ��FBC����$\overrightarrow{AM}=��\overrightarrow{AD}$���M�����꣬�õ�$\overrightarrow{C��M}$����$\overrightarrow{m}•\overrightarrow{C��M}=0$�����жϣ�
��� ��1��֤������BC=CD��EΪBD���е㣬��C��E��BD��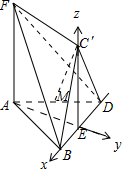
��ƽ��BC'D��ƽ��ABD����ƽ��BC'D��ƽ��ABD=BD��
��C��E��ABD��
��FA��ƽ��ABD����FA��C��E����C��E?ƽ��BC'D��FA?ƽ��BC'D��
��FA��ƽ��BC'D��
��2���⣺��DB����ֱ��Ϊx�ᣬAE����ֱ��Ϊy�ᣬEC������ֱ��Ϊz�Ὠ���ռ�ֱ������ϵ��
��B��1��0��0����A��0��$-\sqrt{3}$��0����D��-1��0��0����F��0��-$\sqrt{3}$��$2\sqrt{3}$����
C�䣨0��0��$\sqrt{3}$����
��$\overrightarrow{BF}=��-1��-\sqrt{3}��2\sqrt{3}��$��$\overrightarrow{BC��}=��-1��0��\sqrt{3}��$��
��ƽ��FBC���һ��������Ϊ$\overrightarrow{m}=��x��y��z��$��
��$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BF}=-x-\sqrt{3}y+2\sqrt{3}z=0}\\{\overrightarrow{m}•\overrightarrow{BC��}=-x+\sqrt{3}z=0}\end{array}\right.$��ȡz=1����$\overrightarrow{m}=��\sqrt{3}��1��1��$��
��ƽ��ABD��һ��������Ϊ$\overrightarrow{n}=��0��1��1��$��
��cos��$\overrightarrow{m}��\overrightarrow{n}$��=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{2}{\sqrt{5}��\sqrt{2}}=\frac{\sqrt{10}}{5}$��
��ƽ��ABD��ƽ��FBC'���ɽǵ�����ֵΪ$\frac{\sqrt{10}}{5}$��
��3���⣺�߶�AD�ϲ����M��ʹ��C'M��ƽ��FBC��
�������߶�AD�ϴ���M��x��y��z����ʹ��C'M��ƽ��FBC��
��$\overrightarrow{AM}=��\overrightarrow{AD}$����x��y$+\sqrt{3}$��z��=�ˣ�-1��$\sqrt{3}$��0��=��-�ˣ�$\sqrt{3}��$��0����
��x=-�ˣ�y=$\sqrt{3}����-1��$��z=0��
��$\overrightarrow{C��M}$=��-�ˣ�$\sqrt{3}����-1��$��-$\sqrt{3}$����
��$\overrightarrow{m}•\overrightarrow{C��M}=0$����$-\sqrt{3}��+\sqrt{3}��-\sqrt{3}=0$����$-\sqrt{3}=0$����
���߶�AD�ϲ����M��ʹ��C'M��ƽ��FBC��
���� ���⿼��ֱ����ƽ��ƽ�е��ж�������ռ�����������˼ά������ѵ�������ÿռ�����������ǵ�ƽ��ǣ����е��⣮

| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
| A�� | $-\frac{{\sqrt{3}}}{2}$ | B�� | $-\frac{1}{2}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{{\sqrt{3}}}{2}$ |
��P��|X-��|���ң�=0.6826��P��|X-��|��2�ң�=0.9544��P��|X-��|��3�ң�=0.9974��
| A�� | 0.6826 | B�� | 0.9544 | C�� | 0.9974 | D�� | 0.3413 |
| A�� | ��ֶ�����Ҫ���� | B�� | ��Ҫ����������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |