题目内容
8.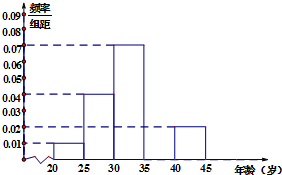 当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取n名市民,按年龄情况进行统计的得到频率分布表和频率分布直方图如下:
当今,手机已经成为人们不可或缺的交流工具,人们常常把喜欢玩手机的人冠上了名号“低头族”,手机已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取n名市民,按年龄情况进行统计的得到频率分布表和频率分布直方图如下:| 组数 | 分组(单位:岁) | 频数 | 频率 |
| 1 | [20,25) | 5 | 0.05 |
| 2 | [25,30) | 20 | 0.20 |
| 3 | [30,35) | a | 0.35 |
| 4 | [35,40) | 30 | b |
| 5 | [40,45] | 10 | 0.10 |
| 合计 | n | 1.00 | |
(2)媒体记者为了做好调查工作,决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访,再从抽出的这20名中年龄在[30,40)的选取2名担任主要发言人.记这2名主要发言人年龄在[35,40)的人数为ξ,求ξ的分布列及数学期望.
分析 (1)由题意可得:n=$\frac{5}{0.05}$=100,可得a=100×0.35,b=$\frac{30}{100}$.
(2)按年龄采用分层抽样的方法在[30,35),(35,40]分别有m,n名,可得:$\frac{20}{100}$=$\frac{m}{35}$=$\frac{n}{30}$,解得m,n,可得年龄在[30,40)共有13名.故ξ的可能取值为0,1,2.利用P(ξ=k)=$\frac{{∁}_{6}^{k}{∁}_{7}^{2-k}}{{∁}_{13}^{2}}$,即可得出分布列与数学期望.
解答 解:(1)由题意可得:n=$\frac{5}{0.05}$=100,∴a=100×0.35=35,b=$\frac{30}{100}$=0.3.
如图所示,
(2)按年龄采用分层抽样的方法在[30,35),
(35,40]分别有m,n名,可得:$\frac{20}{100}$=$\frac{m}{35}$=$\frac{n}{30}$,
解得m=7,n=6,
∴年龄在[30,40)共有13名.故ξ的可能取值为0,1,2.利用P(ξ=k)=$\frac{{∁}_{6}^{k}{∁}_{7}^{2-k}}{{∁}_{13}^{2}}$,可得:P(ξ=0)=$\frac{7}{26}$,
P(ξ=1)=$\frac{7}{13}$,P(ξ=2)=$\frac{5}{26}$.
∴ξ的分布列为:
| ξ | 0 | 1 | 2 |
| P | $\frac{7}{26}$ | $\frac{7}{13}$ | $\frac{5}{26}$ |
点评 本题考查了超几何分布列及其数学期望、频率分布直方图的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.已知1+i=$\frac{i}{z}$,则在复平面内,复数z所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.执行如图所示的程序框图,则输出的结果为( )


| A. | 7 | B. | 9 | C. | 10 | D. | 11 |
20.已知四边形ABCD为梯形,AB∥CD,l为空间一直线,则“l垂直于两腰AD,BC”是“l垂直于两底AB,CD”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.设等差数列{an}的前n项和为Sn,若S9=54,则a1+a5+a9=( )
| A. | 9 | B. | 15 | C. | 18 | D. | 36 |
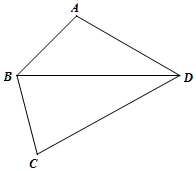 如图,在四边形ABCD中,∠ABD=45°,∠ADB=30°,BC=1,DC=2,cos∠BCD=$\frac{1}{4}$,则BD=2;三角形ABD的面积为$\sqrt{3}$-1.
如图,在四边形ABCD中,∠ABD=45°,∠ADB=30°,BC=1,DC=2,cos∠BCD=$\frac{1}{4}$,则BD=2;三角形ABD的面积为$\sqrt{3}$-1.