题目内容
3.已知△ABC三内角A,B,C对应的边长分别为a,b,c,且$B=\frac{2π}{3}$,又边长b=3c,那么sinC=$\frac{{\sqrt{3}}}{6}$.分析 由已知利用正弦定理即可计算得解.
解答 解:∵$B=\frac{2π}{3}$,又边长b=3c,
∴由正弦定理可得:$\frac{c}{sinC}$=$\frac{b}{sinB}$=$\frac{3c}{sin\frac{2π}{3}}$=$\frac{3c}{\frac{\sqrt{3}}{2}}$,
∴解得:sinC=$\frac{\sqrt{3}}{6}$.
故答案为:$\frac{\sqrt{3}}{6}$.
点评 本题主要考查了正弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
13.已知向量$\overrightarrow a=(m,2)$,$\overrightarrow b=(2,-1)$,且$\overrightarrow a⊥\overrightarrow b$,则$\frac{|2\overrightarrow a-\overrightarrow b|}{\overrightarrow a•(\overrightarrow a+\overrightarrow b)}$等于( )
| A. | $-\frac{5}{3}$ | B. | 1 | C. | 2 | D. | $\frac{5}{4}$ |
18.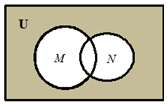 已知全集U是实数集R.如图的韦恩图表示集合M={x|x>2}与N={x|1<x<3}关系,那么阴影部分所表示的集合可能为( )
已知全集U是实数集R.如图的韦恩图表示集合M={x|x>2}与N={x|1<x<3}关系,那么阴影部分所表示的集合可能为( )
 已知全集U是实数集R.如图的韦恩图表示集合M={x|x>2}与N={x|1<x<3}关系,那么阴影部分所表示的集合可能为( )
已知全集U是实数集R.如图的韦恩图表示集合M={x|x>2}与N={x|1<x<3}关系,那么阴影部分所表示的集合可能为( )| A. | {x|x<2} | B. | {x|1<x<2} | C. | {x|x>3} | D. | {x|x≤1} |
20.已知四边形ABCD为梯形,AB∥CD,l为空间一直线,则“l垂直于两腰AD,BC”是“l垂直于两底AB,CD”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
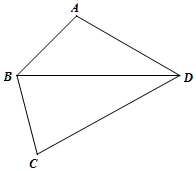 如图,在四边形ABCD中,∠ABD=45°,∠ADB=30°,BC=1,DC=2,cos∠BCD=$\frac{1}{4}$,则BD=2;三角形ABD的面积为$\sqrt{3}$-1.
如图,在四边形ABCD中,∠ABD=45°,∠ADB=30°,BC=1,DC=2,cos∠BCD=$\frac{1}{4}$,则BD=2;三角形ABD的面积为$\sqrt{3}$-1.