题目内容
在△ABC中，“∠C=90°”是“cosA-cosB=sinB-sinA”的（ ）
| A、充分不必要条件 |
| B、充要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据充分条件和必要条件的定义，结合结合三角函数的定义，对选项进行判断
解答：
解：“C=90°”成立时，有A+B=90°，cosA-cosB=cos（90°-B）-cos（90°-A）=sinB-sinA成立，
又当A=B时，cosA-cosB=sinB-sinA，但“C=90°不一定成立，
则在△ABC中充分不必要条件，
故选：A
又当A=B时，cosA-cosB=sinB-sinA，但“C=90°不一定成立，
则在△ABC中充分不必要条件，
故选：A
点评：本题主要考查充分条件和必要条件的判断，解答本题要熟练理解掌握三角函数的定义．
练习册系列答案
相关题目
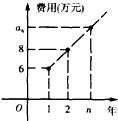为保护环境，绿色出行，某高校今年年初成立自行车租赁公司，初期投入36万元，建成后每年收入25万元，该公司第n年需要付出的维修费用记作an万元，已知{an}为等差数列，相关信息如图所示．两平行直线3x-4y-3=0和6x-8y+5=0之间的距离是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）=
，则f[f(
)]=（ ）
|
| 1 |
| 2 |
| A、-1 | ||
| B、2 | ||
C、
| ||
D、
|
如图，在△ABC中，∠BAC=