题目内容
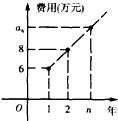 为保护环境,绿色出行,某高校今年年初成立自行车租赁公司,初期投入36万元,建成后每年收入25万元,该公司第n年需要付出的维修费用记作an万元,已知{an}为等差数列,相关信息如图所示.
为保护环境,绿色出行,某高校今年年初成立自行车租赁公司,初期投入36万元,建成后每年收入25万元,该公司第n年需要付出的维修费用记作an万元,已知{an}为等差数列,相关信息如图所示.(1)设该公司前n年总盈利为y万元,试把y表示成n的函数,并求出y的最大值;(总盈利即n年总收入减去成本及总维修费用)
(2)该公司经过几年经营后,年平均盈利最大,并求出最大值.
考点:数列与不等式的综合,函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)由题意知,每年的费用是以6为首项,2为公差的等差数列,即可把y表示成n的函数,利用配方法求出y的最大值;
(2)年平均盈利
=-(n+
)+20,利用基本不等式能求出这种设备使用6年,该公司的年平均获利最大.
(2)年平均盈利
| y |
| n |
| 36 |
| n |
解答:
解:(1)由题意,每年的维修费是以6为首项,2为公差的等差数列,
∴an=a1+2(n-1)=2n+4,
∴y=25n-
-36=-n2+20n-36=-(n-10)2+64
∴n=10时,y的最大值为64万元;
(2)年平均盈利
=-(n+
)+20≤-2
+20=8,
当且仅当n=
,即n=6时,年平均收益最大.
所以这种设备使用6年,该公司的年平均获利最大.
∴an=a1+2(n-1)=2n+4,
∴y=25n-
| n[6+(2n+4)] |
| 2 |
∴n=10时,y的最大值为64万元;
(2)年平均盈利
| y |
| n |
| 36 |
| n |
n×
|
当且仅当n=
| 36 |
| n |
所以这种设备使用6年,该公司的年平均获利最大.
点评:本题考查数列在生产实际中的应用,考查基本不等式的运用,确定函数关系是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
k2,m(m∈N),3,5的平均数为3,平面上的直线l过点(0,1),其斜率为等可能取k的值,用X表示坐标原点到l距离的平方,则随机变量X的数学期望E(X)等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若f(x)=-
x2+(a+2)x+lnx在(1,+∞)上是减函数,则实数a的取值范围是( )
| 1 |
| 2 |
| A、(-∞,-2] |
| B、(-3,-1) |
| C、[-1,0) |
| D、[0,+∞) |
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了下表:
根据表中的数据及随机变量Χ2的公式,算得Χ2≈8.12.临界值表:
根据临界值表,你认为喜爱打篮球与性别之间有关系的把握是( )
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 19 | 6 | 25 |
| 女生 | 9 | 16 | 25 |
| 合计 | 28 | 22 | 50 |
| P(χ2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A、97.5% | B、99% |
| C、99.5% | D、99.9% |
在△ABC中,“∠C=90°”是“cosA-cosB=sinB-sinA”的( )
| A、充分不必要条件 |
| B、充要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
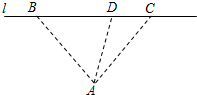 某供货商拟从码头A发货至其对岸l的两个商场B,C处,通常货物先由A处船运至BC之间的中转站D,再利用车辆转运.如图,码头A与两商场B,C的距离相等,两商场间的距离为20千米,且∠BAC=
某供货商拟从码头A发货至其对岸l的两个商场B,C处,通常货物先由A处船运至BC之间的中转站D,再利用车辆转运.如图,码头A与两商场B,C的距离相等,两商场间的距离为20千米,且∠BAC=