在棱长为1的正方体内.有两球相外切.并且又分别与正方体相内切．(1)求两球的半径之和,(2)当两球的半径是多少时.两球体积之和最小．题目和参考答案——青夏教育精英家教网—

题目内容

在棱长为1的正方体内，有两球相外切，并且又分别与正方体相内切．
（1）求两球的半径之和；
（2）当两球的半径是多少时，两球体积之和最小．

考点：球的体积和表面积

专题：空间位置关系与距离

分析：（1）利用ABCD为过球心的对角面，即可求两球半径之和．
（2）表示出两球的体积之和，利用配方法，求两球体积之和最小．

解答： 解：（1）如图，ABCD为过球心的对角面，AC=

，

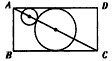
设两球半径为R、r，则有R+r+

（R+r）=

，
所以R+r=

；
（2）设两球的体积之和为V，
则V=

π（R³+r³）=

π•

[3R²-

×R+

(3-

]，
所以当R=r=

时，V有最小值．

点评：本题是基础题，考查棱锥的体积的求法，正方体的内接体的知识，解题关键在八面体转化为两个正四棱锥，是常考题型．

练习册系列答案

已知函数f（x）是定义在R上单调递减的奇函数，则满足不等式f[f（t-1）]＜0的实数t的取值范围是

．

某袋中有10个乒乓球，其中有7个新、3个旧球，从袋中任取3个来用，用后放回袋中（新球用后变为旧球），记此时袋中旧球个数为X，求X的数学期望．

已知定义在R上的函数f（x）对任意实数x、y，恒有f（x）+f（y）=f（x+y），且当x＞0时，有f（x）＜0．
（Ⅰ）求证：f（x）为奇函数且在R上是减函数；
（Ⅱ）若正数x，y满足

=1，且f（x）+f（y）+f（1-m）＜0恒成立，求m的范围．

已知双曲线C：

=1（a＞0，b＞0）的左、右焦点分别为F₁，F₂，过点F₂作双曲线C的一条渐近线的垂线，垂足为H，交双曲线于点M且

，x∈R（其中ω＞0）
（I）求函数f（x）的值域；
（II）若函数y=f（x）的图象与直线y=-1的两个相邻交点间的距离为

，求函数y=f（x）的单调增区间．
（Ⅲ）设g（x）=-4cos²x-sinx+m，若对任意x₁∈R，总是存在x₂∈[0，

]，使得f（x₁）≥g（x₂），求实数m的取值范围．

若函数f（x）=

cosxsin（x+

）．
（Ⅰ）求函数f（x）的最小正周期及最大值；
（Ⅱ）写出函数f（x）在[0，π]上的单调区间．

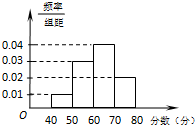在我市2015年“创建文明城市”知识竞赛中，考评组从中抽取200份试卷进行分析，其分数的频率分布直方图如图所示，则分数在区间[60，70）上的人数大约有

人．

试题分类