题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}{-x,-1≤x≤0}\\{{x}^{2},0<x≤1}\\{2x,1<x≤2}\end{array}\right.$,求:(1)f(-$\frac{2}{3}$),f($\frac{1}{2}$),f($\frac{3}{2}$)的值;
(2)作出函数的简图;
(3)求函数的最大值和最小值.
分析 (1)由已知中函数f(x)=$\left\{\begin{array}{l}{-x,-1≤x≤0}\\{{x}^{2},0<x≤1}\\{2x,1<x≤2}\end{array}\right.$,将自变量-$\frac{2}{3}$,$\frac{1}{2}$,$\frac{3}{2}$代入可得f(-$\frac{2}{3}$),f($\frac{1}{2}$),f($\frac{3}{2}$)的值;
(2)根据分段函数分段画的原则,可得函数的简图;
(3)结合(2)中函数的图象,可得函数的最大值和最小值.
解答 解:(1)∵函数f(x)=$\left\{\begin{array}{l}{-x,-1≤x≤0}\\{{x}^{2},0<x≤1}\\{2x,1<x≤2}\end{array}\right.$,
∴f(-$\frac{2}{3}$)=$\frac{2}{3}$,
f($\frac{1}{2}$)=$\frac{1}{4}$,
f($\frac{3}{2}$)=$\frac{3}{2}$;
(2)函数f(x)的图象如下图所示: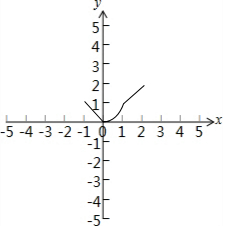
(3)由函数的图象可得:
当x=2时,函数取最大值2,
当x=0时,函数取最小值0.
点评 本题考查的知识点是分段函数的应用,函数求值,函数的图象,函数的最值及其几何意义,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知f:A→B为从集合A到集合B的一个映射,A=B={(x,y)|x∈R,y∈R},f:(x,y)→(x+y,x-y),若A中元素(1,a)的象是(b,4),则实数a,b的值分别为( )
| A. | -2,3 | B. | -2,-3 | C. | -3,-2 | D. | 1,4 |