题目内容
10.设F是椭圆$\frac{x^2}{9}$+$\frac{y^2}{8}$=1的右焦点,点A(1,2),M是椭圆上一动点,则MA+MF取值范围为(6-2$\sqrt{2}$,6+2$\sqrt{2}$).分析 椭圆左焦点设为F1,连接MF1.利用椭圆的定义以及在三角形中,两边之差总小于第三边,当A、M、F1成一直线时,|MA|-|MF1|最大,求解即可.利用|MA|+|MF2|=|MA|+6-|MF1|=10-(|MF1|-|MA|)≥6-|AF1|,即可得出其最小值.
解答 解:由椭圆$\frac{x^2}{9}$+$\frac{y^2}{8}$=1的焦点在x轴上,a=3,b=2$\sqrt{2}$,c=1,
左焦点为F1(-1,0),连接MF1.
由椭圆的定义可知:|MF1|+|MF|=2a,
|MA|+|MF|=|MA|+2a-|MF1|=6+|MA|-|MF1|.
即|MA|-|MF1|最大时,|MA|+|MF2|最大.
在△AMF1中,两边之差总小于第三边,所以当A、M、F1成一直线时,|MA|-|MF1|最大,
|MA|-|MF1|=|AF1|=$\sqrt{(1+1)^{2}+(2-0)^{2}}$=2$\sqrt{2}$.
∴|MA|+|MF2|的最大值是6+2$\sqrt{2}$.
∴|MA|+|MF2|=|MA|+6-|MF1|=6-(|MF1|-|MA|)≥10-|AF1|=6-2$\sqrt{2}$,
∴|MA|+|MF|的取值范围(6-2$\sqrt{2}$,6+2$\sqrt{2}$),
故答案为:(6-2$\sqrt{2}$,6+2$\sqrt{2}$).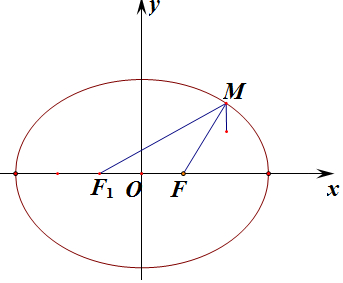
点评 本题主要考查圆锥曲线的定义的应用,在解决涉及到圆锥曲线上的点与焦点之间的关系的问题中,考查数形结合思想的应用,属于中档题.

练习册系列答案
相关题目
18.已知角α的终边上一点P(-$\sqrt{3}$,m),且sinα=$\frac{\sqrt{2}m}{4}$,则实数m的值为( )
| A. | $\sqrt{5}$或-$\sqrt{5}$ | B. | $\sqrt{5}$或0 | C. | -$\sqrt{5}$或0 | D. | 0或$\sqrt{5}$或-$\sqrt{5}$ |
5.已知{an}是公差为1的等差数列,Sn为{an}的前n项和,若S8=4S4,则a9等于( )
| A. | $\frac{17}{2}$ | B. | $\frac{19}{2}$ | C. | 9 | D. | 10 |
19.直线x+$\sqrt{2}$y-1=0的斜率是( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
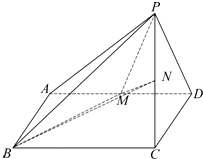 四棱锥P-ABCD中,PC=AB=1,BC=2,∠ABC=60°,底面ABCD为平行四边形,PC⊥平面ABCD,点M,N分别为AD,PC的中点.
四棱锥P-ABCD中,PC=AB=1,BC=2,∠ABC=60°,底面ABCD为平行四边形,PC⊥平面ABCD,点M,N分别为AD,PC的中点.