题目内容
14.为了考察某校各班参加课外书法小组的人数,从全校随机抽取5个班级,把每个班级参加该小组的人数作为样本数据.已知样本平均数为7,样本方差为4,且样本数据互不相同,则样本数据中的最大值为( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 运用平均数公式求出平均数,再运用方差的公式列出方差表达式,再讨论样本数据中的最大值的情况,即可解决问题
解答 解:设样本数据为:x1,x2,x3,x4,x5,
平均数=(x1+x2+x3+x4+x5)÷5=7;
方差s2=[(x1-7)2+(x2-7)2+(x3-7)2+(x4-7)2+(x5-7)2]÷5=4.
从而有x1+x2+x3+x4+x5=35,①
(x1-7)2+(x2-7)2+(x3-7)2+(x4-7)2+(x5-7)2=20.②
若样本数据中的最大值为11,不妨设x5=11,则②式变为:
(x1-7)2+(x2-7)2+(x3-7)2+(x4-7)2=4,由于样本数据互不相同,这是不可能成立的;
若样本数据为4,6,7,8,10,代入验证知①②式均成立,此时样本数据中的最大值为 10.
故答案为:10.
点评 本题考查的是平均数和方差的求法,记住公式 是关键,同时也考查了分析问题的能力,属于中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
5.已知{an}是公差为1的等差数列,Sn为{an}的前n项和,若S8=4S4,则a9等于( )
| A. | $\frac{17}{2}$ | B. | $\frac{19}{2}$ | C. | 9 | D. | 10 |
19.直线x+$\sqrt{2}$y-1=0的斜率是( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
3.命题“?x∈R,x2=x”的否定是( )
| A. | ?x∉R,x2≠x | B. | ?x∈R,x2≠x | C. | ?x∉R,x2≠x | D. | ?x∈R,x2≠x |
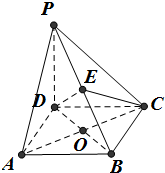 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2${\sqrt{3}^{\;}}$,且AC,BD交于点O,E是PB上任意一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2${\sqrt{3}^{\;}}$,且AC,BD交于点O,E是PB上任意一点.