题目内容
3.有以下命题:①若函数f(x)既是奇函数又是偶函数,则f(x)的值域为{0};
②若函数f(x)是偶函数,则f(|x|)=f(x);
③若函数f(x)在其定义域内不是单调函数,则f(x)不存在反函数;
④若函数f(x)存在反函数f-1(x),且f-1(x)与f(x)不完全相同,则f(x)与f-1(x)图象的公共点必在直线y=x上;
其中真命题的序号是①②.(写出所有真命题的序号)
分析 ①函数f(x)既是奇函数又是偶函数,则f(x)=0.②利用偶函数的定义和性质判断.③利用单调函数的定义进行判断.④利用反函数的性质进行判断.
解答 解:①若函数f(x)既是奇函数又是偶函数,则f(x)=0,为常数函数,所以f(x)的值域是{0},
所以①正确.
②若函数为偶函数,则f(-x)=f(x),所以f(|x|)=f(x)成立,所以②正确.
③因为函数f(x)=$\frac{1}{x}$在定义域上不单调,但函数f(x)存在反函数,所以③错误.
④原函数图象与其反函数图象的交点关于直线y=x对称,但不一定在直线y=x上,
比如函数y=-$\sqrt{x+1}$与其反函数y=x2-1(x≤0)的交点坐标有(-1,0),(0,1),
显然交点不在直线y=x上,所以④错误.
故答案为:①②.
点评 本题主要考查函数的有关性质的判定和应用,要求熟练掌握相应的函数的性质,综合性较强.

练习册系列答案
相关题目
14.已知双曲线方程为x2-y2=4,过点A(3,1)作直线l与该双曲线交于M,N两点,若点A恰好为MN中点,则直线l的方程为( )
| A. | y=3x-8 | B. | y=-3x+8 | C. | y=3x-10 | D. | y=-3x+10 |
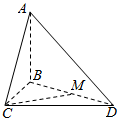 如图,已知AB⊥平面BCD,BC⊥CD,AD与平面BCD所成的角为30°,且AB=BC=2;
如图,已知AB⊥平面BCD,BC⊥CD,AD与平面BCD所成的角为30°,且AB=BC=2;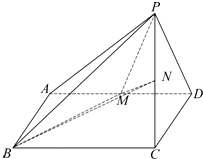 四棱锥P-ABCD中,PC=AB=1,BC=2,∠ABC=60°,底面ABCD为平行四边形,PC⊥平面ABCD,点M,N分别为AD,PC的中点.
四棱锥P-ABCD中,PC=AB=1,BC=2,∠ABC=60°,底面ABCD为平行四边形,PC⊥平面ABCD,点M,N分别为AD,PC的中点.