题目内容

17．已知f：A→B为从集合A到集合B的一个映射，A=B={（x，y）|x∈R，y∈R}，f：（x，y）→（x+y，x-y），若A中元素（1，a）的象是（b，4），则实数a，b的值分别为（　　）
A．-2，3B．-2，-3C．-3，-2D．1，4

分析 （x，y）在映射f下的象是（x+y，x-y），由此运算规则求（1，a）在f下的象；再根据A中元素（1，a）的象是（b，4），即可得出结论．

解答 解：∵A=B={（x，y）|x∈R，y∈R}，f（x，y）→（x+y，x-y）．
∴A中元素（1，a）的象是1+a，1-a，
∵A中元素（1，a）的象是（b，4），
∴$\left\{\begin{array}{l}{1+a=b}\\{1-a=4}\end{array}\right.$，∴a=-3．b=-2．
故选C．

点评 本题考查映射，解题的关键是理解所给的映射规则，根据此规则建立方程求出原象．

练习册系列答案
相关题目
18．若函数f（x）=log2（x+1）+a的反函数的图象经过点（4，1），则实数a=3．
8．在等比数列{an}中，a1=1，a10=3，则a2a3…a8a9等于（　　）
A．243B．$27\root{5}{27}$C．$\sqrt{3}$D．81
5．已知{an}是公差为1的等差数列，Sn为{an}的前n项和，若S8=4S4，则a9等于（　　）
A．$\frac{17}{2}$B．$\frac{19}{2}$C．9D．10
12．已知下列命题：
①“M＞N”是“（$\frac{2}{3}$）M＜（$\frac{2}{3}$）N”的充要条件．
②若函数y=f（x+1）为偶函数，则y=f（x）的图象关于x=1对称；
③命题p：“?x∈R，x2-2≥0”的否定形式为非p：“?x∈R，x2-2＜0”；
④命题“若x≠y，则sin x≠sin y”的逆否命题为真命题
其中正确的命题序号是①②③．
2．已知函数f（x）=$\left\{\begin{array}{l}{-x，-1≤x≤0}\\{{x}^{2}，0＜x≤1}\\{2x，1＜x≤2}\end{array}\right.$，求：
（1）f（-$\frac{2}{3}$），f（$\frac{1}{2}$），f（$\frac{3}{2}$）的值；
（2）作出函数的简图；
（3）求函数的最大值和最小值．
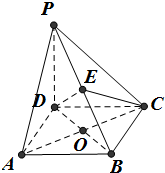9．如图，在四棱锥P-ABCD中，PD⊥平面ABCD，四边形ABCD是菱形，AC=2，BD=2${\sqrt{3}^{\;}}$，且AC，BD交于点O，E是PB上任意一点．
（1）求证：AC⊥DE；
（2）若E为PB的中点，且二面角A-PB-D的余弦值为$\frac{{\sqrt{21}}}{7}$，求EC与平面PAB所成角θ的正弦值．
6．设函数f（x）=$\left\{\begin{array}{l}{3x+\frac{5}{2}，x＜1}\\{{2}^{x}，x≥1}\end{array}\right.$，则满足f（f（a））=2f（a）的a的取值范围是[-$\frac{1}{2}$，+∞）．
7．某工厂经过市场调查，甲产品的日销售量P（单位：吨）与销售价格x（单位：万元/吨）满足关系式P=$\left\{\begin{array}{l}{-ax+17，3＜x≤6}\\{\frac{84}{{x}^{2}}+\frac{7}{x}，6＜x≤9}\end{array}\right.$（其中a为常数），已知销售价格为4万元/吨时，每天可售出该产品9吨．
（1）求a的值；
（2）若该产品的成本价格为3万元/吨，当销售价格为多少时，该产品每天的利润最大？并求出最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网