题目内容
7.线性约束条件$\left\{\begin{array}{l}{x-y≤0}\\{2x-y≥0}\\{x+y-1≤0}\end{array}\right.$表示平面区域D,若在区域D上有无穷多个点(x,y),可使目标函数z=x+my取得最大值,则m=1或-1.分析 由约束条件作差可行域,化目标函数为直线方程的斜截式,然后分m>0和m<0分类求解得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x-y≤0}\\{2x-y≥0}\\{x+y-1≤0}\end{array}\right.$作出平面区域D: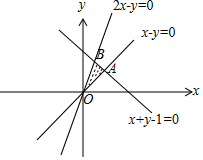
化目标函数z=x+my为$y=-\frac{1}{m}x+\frac{z}{m}$,
当m>0时,要使目标函数z=x+my取得最大值的点(x,y)有无穷多个,则$-\frac{1}{m}=-1$,得m=1;
当m<0时,要使目标函数z=x+my取得最大值的点(x,y)有无穷多个,则$-\frac{1}{m}=1$,得m=-1.
故答案为:1或-1.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
18.已知角α的终边上一点P(-$\sqrt{3}$,m),且sinα=$\frac{\sqrt{2}m}{4}$,则实数m的值为( )
| A. | $\sqrt{5}$或-$\sqrt{5}$ | B. | $\sqrt{5}$或0 | C. | -$\sqrt{5}$或0 | D. | 0或$\sqrt{5}$或-$\sqrt{5}$ |
19.直线x+$\sqrt{2}$y-1=0的斜率是( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
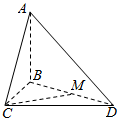 如图,已知AB⊥平面BCD,BC⊥CD,AD与平面BCD所成的角为30°,且AB=BC=2;
如图,已知AB⊥平面BCD,BC⊥CD,AD与平面BCD所成的角为30°,且AB=BC=2;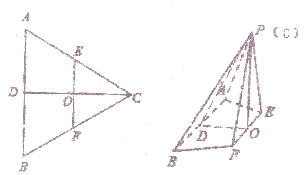 如图,在边长为4的等边三角形ABC中,点D,E,F分别是边AB,AC,BC的中点,DC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的四棱锥P-ABFE,且PB=$\sqrt{10}$.
如图,在边长为4的等边三角形ABC中,点D,E,F分别是边AB,AC,BC的中点,DC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的四棱锥P-ABFE,且PB=$\sqrt{10}$.