题目内容

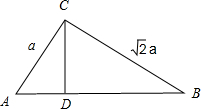在Rt△ABC中，两直角边的长分别为AC=a，BC=
2
a，沿斜边AB上的高CD将平面ACD折到平面A′CD，使平面A′CD⊥平面BCD，求折叠后点D到平面A′BC的距离．
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：由VC-BDA′=VD-BCA′，设折叠后点D到平面A′BC的距离为h，利用等积法能求出折叠后点D到平面A′BC的距离．
解答： 解：∵Rt△ABC中，两直角边的长分别为AC=a，BC=
2
a，
斜边AB上的高是CD，
∴A′D=
3
3
a，BD=
2
3
3
a，CD=
6
3
a，A′B=
15
3
a，
∴cos∠A′CB=
a2+2a2-
15
9
a2
2
2
a2
=
2
3
，
∴sin∠A′CB=
1-
2
9
=
7
3
，
∴S△A′CB=
1
2
a•
2
a•
7
3
=
14
6
a2，
∵VC-BDA′=VD-BCA′，
设折叠后点D到平面A′BC的距离为h，
∴
1
3
×
2
3
3
a×
3
3
a×
6
3
a=
1
3
×
14
6
a2•h，
解得h=
4
21
21
．
∴折叠后点D到平面A′BC的距离是
4
21
21
．
点评：本题考查点到平面的距离的求法，是中档题，解题时要认真审题，注意等积法的合理运用．
练习册系列答案
相关题目
已知直线l，平面α、β，若l⊥α，l⊥β，求证：α∥β．
已知正项数列{an}的前n项和Sn满足：Sn2-（n2+2n-3）Sn-3（n2+2n）=0（n∈N*）
（Ⅰ）求证：Sn=n2+2n；
（Ⅱ）求数列{
1
Sn
}的前n项和Tn．
在平面直角坐标系xOy中，设动点P，Q都在曲线C：
x=1+2cosθ 
y=2sinθ
（θ为参数）上，且这两点对应的参数分别为θ=α与θ=2α（0＜α＜2π），设PQ的中点M与定点A（1，0）间的距离为d，求d的取值范围．
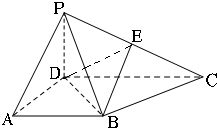如图，在四棱锥P-ABCD中，PD⊥平面ABCD，AB∥CD，AD⊥CD，且AB=AD=PD=1，CD=2，E为PC的中点．
（Ⅰ）求证：BE∥平面PAD；
（Ⅱ）求二面角E-BD-C的余弦值．
如果函数y=
2kx+1
kx2+4kx+3
的定义域为R，则实数k的取值范围
 
．
若变量x，y满足约束条件
x+y-3≤0
x-y+1≥0
y≥1
，则z=|y-2x|的最大值为
 
．
设a＞b＞c＞0，则2a2+
1
ab
+
1
a(a-b)
-10ac+25c2取最小值时abc=
 
．
一块各面均有油漆的正方体被锯成1000个大小相同的小正方体，若将这些小正方体均匀混在一起，则任意取出一个正方体，其三面涂有油漆的概率是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网