题目内容
一块各面均有油漆的正方体被锯成1000个大小相同的小正方体,若将这些小正方体均匀混在一起,则任意取出一个正方体,其三面涂有油漆的概率是 .
考点:古典概型及其概率计算公式
专题:概率与统计
分析:由于试验发生包含的基本事件数是1000,先列举出符合题意的情况的个数,再根据概率公式解答即可.
解答:
解:由题意知本题是一个古典概型,由于试验发生包含的基本事件数是1000,
而满足条件的事件是三面涂有油漆的小正方形个数,
由于三面涂有油漆的小正方形只能位于大正方形的8个顶点处,
故三面涂有油漆的概率是
=
,
故答案为:
.
而满足条件的事件是三面涂有油漆的小正方形个数,
由于三面涂有油漆的小正方形只能位于大正方形的8个顶点处,
故三面涂有油漆的概率是
| 8 |
| 1000 |
| 1 |
| 125 |
故答案为:
| 1 |
| 125 |
点评:本题考查古典概型,是一个可以通过计算得到满足条件的事件数的题目,解题的关键是数清楚三面染色的小正方形的块数,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合M={1,3,5},N={-2,0,2,4},定义函数f:M→N.若点A(1,f(1))、B(3,f(3))、C(5,f(5)),△ABC的外接圆圆心为D,且
+
=λ
(λ∈R),则满足条件的函数f(x)有( )
| DA |
| DC |
| DB |
| A、6个 | B、10个 |
| C、12个 | D、16个 |
设实数x,y满足
,目标函数u=y-2x的最大值为( )
|
| A、1 | B、3 | C、5 | D、7 |
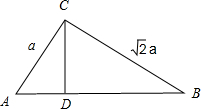 在Rt△ABC中,两直角边的长分别为AC=a,BC=
在Rt△ABC中,两直角边的长分别为AC=a,BC= 如图,正方体ABCD-A1B1C1D1中,E,F分别是面A1B1C1D1和AA1D1D的中心,则EF和CD所成的角是
如图,正方体ABCD-A1B1C1D1中,E,F分别是面A1B1C1D1和AA1D1D的中心,则EF和CD所成的角是