题目内容
在△ABC中,角A、B、C所对的边分别为a、b、c,已知向量
=(cosA,cosB),
=(2c+b,a),且
⊥
.
(Ⅰ) 求角A的大小;
(Ⅱ) 若a=4
,b+c=8,求△ABC的面积.
| m |
| n |
| m |
| n |
(Ⅰ) 求角A的大小;
(Ⅱ) 若a=4
| 3 |
考点:正弦定理,平面向量数量积的运算,余弦定理
专题:解三角形
分析:(Ⅰ)由向量垂直求得等式(2c+b)•cosA+acosB=0,利用正弦定理把边转化成角的正弦整理求得cosA的值,继而求得A.
(Ⅱ)由余弦定理和已知条件求得bc,最后根据三角形面积公式求得答案.
(Ⅱ)由余弦定理和已知条件求得bc,最后根据三角形面积公式求得答案.
解答:
解:(Ⅰ)∵
⊥
.
∴
•
=(2c+b)•cosA+acosB=0,
由正弦定理可得(2sinC+sinB)cosA+sinAcosB=0
整理得sinC+2sinCcosA=0
∵0<C<π,sinC>0,
∴cosA=-
,A=
(II)由余弦定理可得 a2=b2+c2-2bccosA,
48=b2+c2-bc=(b+c)2-bc=64-bc,即bc=16
故S=
bcsinA=
×16×
=4
.
| m |
| n |
∴
| m |
| n |
由正弦定理可得(2sinC+sinB)cosA+sinAcosB=0
整理得sinC+2sinCcosA=0
∵0<C<π,sinC>0,
∴cosA=-
| 1 |
| 2 |
| 2π |
| 3 |
(II)由余弦定理可得 a2=b2+c2-2bccosA,
48=b2+c2-bc=(b+c)2-bc=64-bc,即bc=16
故S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
点评:本题主要考查了正弦定理和余弦定理的应用,平面向量的基本知识.利用正弦定理和余弦定理进行三角形边角问题的转化.

练习册系列答案
相关题目
在极坐标系中,过点(2,
)且与极轴平行的直线方程是( )
| π |
| 2 |
| A、ρ=2 | ||
B、θ=
| ||
| C、ρcosθ=2 | ||
| D、ρsinθ=2 |
 已知三棱锥的底面是边长为2的正三角形,其正(主)视图与俯视图如图所示,则其侧(左)视图的面积为( )
已知三棱锥的底面是边长为2的正三角形,其正(主)视图与俯视图如图所示,则其侧(左)视图的面积为( )A、
| ||
B、
| ||
| C、3 | ||
D、2
|
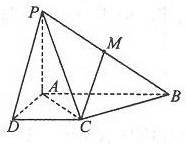 已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,M为PB中点.
已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,M为PB中点. 已知长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=5,P是棱CC1上的任意一点,试问:当点P在哪个位置时,AP⊥平面A1BD?
已知长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=5,P是棱CC1上的任意一点,试问:当点P在哪个位置时,AP⊥平面A1BD?