题目内容
 已知长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=5,P是棱CC1上的任意一点,试问:当点P在哪个位置时,AP⊥平面A1BD?
已知长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=5,P是棱CC1上的任意一点,试问:当点P在哪个位置时,AP⊥平面A1BD?考点:直线与平面垂直的判定
专题:空间位置关系与距离
分析:连接AC交BD于O,连接AC1,先证明出BD⊥平面ACC1,进而可推断出BD⊥AC1,同理证明出AC1⊥A1B,最后根据线面垂直的判定定理证明出AC1⊥平面A1BD,即AP⊥平面A1BD.
解答:
解:P与C1重合时有AP⊥平面A1BD,
证明如下,
连接AC交BD于O,连接AC1,
∵AB=BC,四边形ABCD为平行四边形,
∴四边形ABCD为正方形,
∴AC⊥BD,
∵CC1⊥面ABCD,BD?面ABCD,
∴CC1⊥BD,
∵CC1?平面ACC1,AC?平面ACC1,CC1∩AC=C,
∴BD⊥平面ACC1,
∵AC1?平面ACC1,
∴BD⊥AC1,
同理AC1⊥A1B,
∴AC1⊥平面A1BD,
P与C1重合,
∴AP⊥平面A1BD.
证明如下,
连接AC交BD于O,连接AC1,
∵AB=BC,四边形ABCD为平行四边形,
∴四边形ABCD为正方形,
∴AC⊥BD,
∵CC1⊥面ABCD,BD?面ABCD,
∴CC1⊥BD,
∵CC1?平面ACC1,AC?平面ACC1,CC1∩AC=C,
∴BD⊥平面ACC1,
∵AC1?平面ACC1,
∴BD⊥AC1,
同理AC1⊥A1B,
∴AC1⊥平面A1BD,
P与C1重合,
∴AP⊥平面A1BD.
点评:本题主要考查了线面垂直的判定定理和线面垂直的性质.解题的关键找到与面垂直的直线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
请仔细观察,运用合情推理,写在下面括号里的数最可能的是1,1,2,3,5,( ),13.
| A、8 | B、9 | C、10 | D、11 |
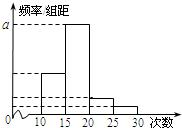 对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图: