题目内容
解关于x的不等式：x3-2x2-5x+6＜0．
考点：其他不等式的解法
专题：不等式的解法及应用
分析：把不等式变形为（x3-x2）-（x2+5x-6）＜0，把左边每一组分别提取公因式，接着再提取公因式化为（x+1）（x+2）（x-3）＜0，再用穿根法求得它的解集．
解答：
解：不等式x3-2x2-5x+6＜0，
即 （x3-x2）-（x2+5x-6）＜0，
即 x2（x-1）-（x-1）（x+6）＜0，即（x-1）（x2-x-6）＜0，
即（x+1）（x+2）（x-3）＜0，
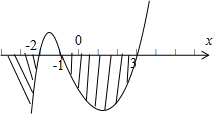
把各个因式的根-1、-2、3排列在数轴上，
用穿根法求得它的解集为 {x|x＜-2，或-1＜x＜3}．
解：不等式x3-2x2-5x+6＜0，即 （x3-x2）-（x2+5x-6）＜0，
即 x2（x-1）-（x-1）（x+6）＜0，即（x-1）（x2-x-6）＜0，
即（x+1）（x+2）（x-3）＜0，
把各个因式的根-1、-2、3排列在数轴上，
用穿根法求得它的解集为 {x|x＜-2，或-1＜x＜3}．
点评：此题主要考查了利用分组分解法分解因式，其中直接分组分解困难，由式子的特点易想到提取公因式法，关键是将二次项拆成几个代数式的和，以便凑配，属于基础题．
练习册系列答案
53随堂测系列答案
相关题目
一个四棱锥的侧棱长都相等，底面是正方形，其正视图如图所示，则四棱锥的表面积为（ ）
A、
| ||
B、4
| ||
C、4
| ||
D、4（
|
自然数列按如图规律排列，若2013在第m行第n个数，则
=（ ）
1
3 2
4 5 6
10 9 8 7
11 12 13 14 15
…
| n |
| m |
1
3 2
4 5 6
10 9 8 7
11 12 13 14 15
…
A、
| ||
B、
| ||
C、
| ||
D、
|
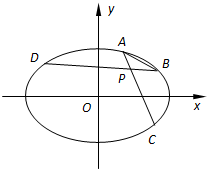如图所示，在平面直角坐标系xOy中，设椭圆E：
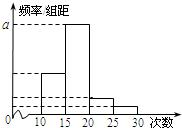对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如图：