题目内容
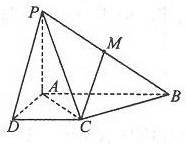 已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,M为PB中点.
已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,M为PB中点.(Ⅰ)求证:MC∥平面PAD;
(Ⅱ)求证:BC⊥平面PAC.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)取PA的中点N,连接MN,DN,先证明出四边形DCMN为平行四边形,进而推断出MC∥DN,根据线面平行的判定定理证明出MC∥平面PAD.
(Ⅱ)求得AC的长,进而利用勾股定理证明BC⊥AC,根据线面垂直的性质推断出PA⊥BC,最后根据线面垂直的判定定理证明出BC⊥平面PAC.
(Ⅱ)求得AC的长,进而利用勾股定理证明BC⊥AC,根据线面垂直的性质推断出PA⊥BC,最后根据线面垂直的判定定理证明出BC⊥平面PAC.
解答:
 证明:(Ⅰ)取PA的中点N,连接MN,DN,
证明:(Ⅰ)取PA的中点N,连接MN,DN,
∵M,N分别时PB,PA的中点,
∴MN∥AB,MN=
AB,
∵CD∥AB,CD=1,AB=2,
∴CD∥AB,CD=
AB,
∴MN∥CD,CD=MN,
∴四边形DCMN为平行四边形,
∴MC∥DN,
∵MC?平面PAD,DN?平面PAD,
∴MC∥平面PAD.
(Ⅱ)在直角梯形ABCD中,过C作CE⊥AB=E,
则四边形ADCE为矩形,
∴AE=CD=1,
∵AB=2,
∴BE=1,
在Rt△BEC中,∠ABC=45°,
∴CE=BE=1,CB=
,
则AC=
=
,
∴AC2+BC2=AB2,
∴BC⊥AC,
∵PA⊥平面ABCD,BC?平面ABCD,
∴PA⊥BC,
∵PA∩AC=A,
∴BC⊥平面PAC.
 证明:(Ⅰ)取PA的中点N,连接MN,DN,
证明:(Ⅰ)取PA的中点N,连接MN,DN,∵M,N分别时PB,PA的中点,
∴MN∥AB,MN=
| 1 |
| 2 |
∵CD∥AB,CD=1,AB=2,
∴CD∥AB,CD=
| 1 |
| 2 |
∴MN∥CD,CD=MN,
∴四边形DCMN为平行四边形,
∴MC∥DN,
∵MC?平面PAD,DN?平面PAD,
∴MC∥平面PAD.
(Ⅱ)在直角梯形ABCD中,过C作CE⊥AB=E,
则四边形ADCE为矩形,
∴AE=CD=1,
∵AB=2,
∴BE=1,
在Rt△BEC中,∠ABC=45°,
∴CE=BE=1,CB=
| 2 |
则AC=
| AD2+CD2 |
| 2 |
∴AC2+BC2=AB2,
∴BC⊥AC,
∵PA⊥平面ABCD,BC?平面ABCD,
∴PA⊥BC,
∵PA∩AC=A,
∴BC⊥平面PAC.
点评:本题主要考查了线面平行和线面垂直的判定定理的应用,考查了学生空间观察能力和推理能力.

练习册系列答案
相关题目
已知A(1,0),点B在曲线G:y=lnx上,若线段AB与曲线M:y=
相交且交点恰为线段AB的中点,则称B为曲线G关于曲线M的一个关联点.那么曲线G关于曲线M的关联点的个数为( )
| 1 |
| x |
| A、0 | B、1 | C、2 | D、4 |
自然数列按如图规律排列,若2013在第m行第n个数,则
=( )
1
3 2
4 5 6
10 9 8 7
11 12 13 14 15
…
| n |
| m |
1
3 2
4 5 6
10 9 8 7
11 12 13 14 15
…
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,在平面直角坐标系xOy中,设椭圆E:
如图所示,在平面直角坐标系xOy中,设椭圆E: 对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图: