题目内容
f(x)=x2+ax+b有两个零点m,n,证明:若|a|+|b|<1,则|m|<1,|n|<1.
考点:二次函数的性质
专题:函数的性质及应用,不等式的解法及应用
分析:由函数的零点与方程实数根的关系,以及根与系数的关系得出m+n=-a,mn=b;再利用绝对值与不等式证明出结论即可.
解答:
证明:∵f(x)=x2+ax+b有两个零点m,n,
即方程x2+ax+b=0有两个实根m,n;
∴m+n=-a,mn=b;
即|m+n|=|a|,|m||n|=|b|;
又∵|a|+|b|<1,
∴|m+n|+|m||n|=|a|+|b|<1;
又∵|m|-|n|≤|m+n|,
∴|m|-|n|+|m||n|<1,
∴(|m|-1)(|n|+1)<0,
即|m|<1,
同理|n|<1.
即方程x2+ax+b=0有两个实根m,n;
∴m+n=-a,mn=b;
即|m+n|=|a|,|m||n|=|b|;
又∵|a|+|b|<1,
∴|m+n|+|m||n|=|a|+|b|<1;
又∵|m|-|n|≤|m+n|,
∴|m|-|n|+|m||n|<1,
∴(|m|-1)(|n|+1)<0,
即|m|<1,
同理|n|<1.
点评:本题考查了函数的零点与对应方程实数根的关系以及不等式的证明问题,是综合性题目.

练习册系列答案
相关题目
已知集合M={x|-1<x<1},N={x|3x>1},则M∩N=( )
| A、∅ |
| B、{x|x>0} |
| C、{x|x<1} |
| D、{x|0<x<1} |
 为了了解某校今年高三男生的身体状况,随机抽查了部分男生,将测得的他们的体重(单位:千克)数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了了解某校今年高三男生的身体状况,随机抽查了部分男生,将测得的他们的体重(单位:千克)数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.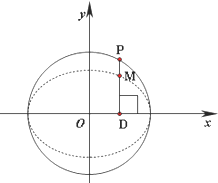 如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且
如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且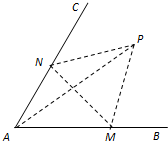 如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).