题目内容
已知函数f(x)=x2-mx+m-1,若对于区间[2,
]内任意两个相异实数x1,x2,总有|f(x1)-f(x2)|≤|x1-x2|成立,求实数m的取值范围.
| 5 |
| 2 |
考点:二次函数的性质
专题:导数的概念及应用
分析:由已知中对于区间[2,
]内任意两个相异实数x1,x2,总有|f(x1)-f(x2)|≤|x1-x2|成立可得:在区间[2,
]内|f′(x)|=
=|2x-m|≤1恒成立,进而可得实数m的取值范围.
| 5 |
| 2 |
| 5 |
| 2 |
| |f(x1)-f(x2)| |
| |x1-x2| |
解答:
解:∵f(x)=x2-mx+m-1,
∴f′(x)=2x-m,
若对于区间[2,
]内任意两个相异实数x1,x2,总有|f(x1)-f(x2)|≤|x1-x2|成立,
即对于区间[2,
]内任意两个相异实数x1,x2,总有|f′(x)|=
≤1
即在区间[2,
]内|2x-m|≤1恒成立
即
在区间[2,
]上恒成立
∴即
在区间[2,
]上恒成立
∴4≤m≤5.
故实数m的取值范围为[4,5].
∴f′(x)=2x-m,
若对于区间[2,
| 5 |
| 2 |
即对于区间[2,
| 5 |
| 2 |
| |f(x1)-f(x2)| |
| |x1-x2| |
即在区间[2,
| 5 |
| 2 |
即
|
| 5 |
| 2 |
∴即
|
| 5 |
| 2 |
∴4≤m≤5.
故实数m的取值范围为[4,5].
点评:本题考查的知识点是导数的几何意义,其中根据已知得到在区间[2,
]内|f′(x)|=
=|2x-m|≤1恒成立,是解答的关键.
| 5 |
| 2 |
| |f(x1)-f(x2)| |
| |x1-x2| |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为了了解某校今年高三男生的身体状况,随机抽查了部分男生,将测得的他们的体重(单位:千克)数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了了解某校今年高三男生的身体状况,随机抽查了部分男生,将测得的他们的体重(单位:千克)数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.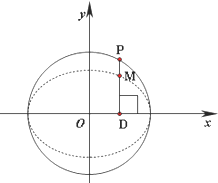 如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且
如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且